题目内容
8.若x,y满足不等式组$\left\{\begin{array}{l}3x-4≥0\\ y≥1\\ 3x+y-6≤0\end{array}\right.$,表示平面区域为D,已知点O(0,0),A(1,0),点M是D上的动点,$\overrightarrow{OA}•\overrightarrow{OM}=λ|\overrightarrow{OM}|$,则λ的最大值为$\frac{{5\sqrt{34}}}{34}$.分析 作出可行域,由题意和数量积的运算可得λ=$\sqrt{\frac{1}{1+(\frac{y}{x})^{2}}}$,数形结合由斜率的意义求出k=$\frac{y}{x}$的最小值可得.
解答 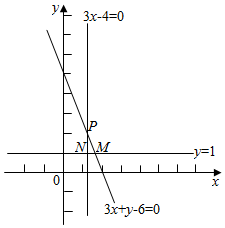 解:作出不等式组$\left\{\begin{array}{l}3x-4≥0\\ y≥1\\ 3x+y-6≤0\end{array}\right.$所对应的可行域D(如图△MNP),
解:作出不等式组$\left\{\begin{array}{l}3x-4≥0\\ y≥1\\ 3x+y-6≤0\end{array}\right.$所对应的可行域D(如图△MNP),
由题意可得$\overrightarrow{OA}$=(1,0),设M(x,y),则$\overrightarrow{OM}$=(x,y),
∴$\overrightarrow{OA}•\overrightarrow{OM}=λ|\overrightarrow{OM}|$可化为x=λ$\sqrt{{x}^{2}+{y}^{2}}$,
则λ=$\frac{x}{\sqrt{{x}^{2}+{y}^{2}}}$=$\sqrt{\frac{{x}^{2}}{{x}^{2}+{y}^{2}}}$=$\sqrt{\frac{1}{1+(\frac{y}{x})^{2}}}$,
数形结合可知当取区域中的点M($\frac{5}{3}$,1)与原点连线的斜率k=$\frac{y}{x}$取最小值$\frac{3}{5}$,
λ=$\sqrt{\frac{1}{1+(\frac{y}{x})^{2}}}$取最大值$\sqrt{\frac{1}{1+(\frac{3}{5})^{2}}}$=$\frac{{5\sqrt{34}}}{34}$,
故答案为:$\frac{{5\sqrt{34}}}{34}$.
点评 本题考查简单线性规划,准确作图并变形目标函数利用斜率的范围是解决问题的关键,属中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
19.已知复数z满足z(1+i)=1(i为虚数单位),则z=( )
| A. | $\frac{1-i}{2}$ | B. | $\frac{1+i}{2}$ | C. | 1-i | D. | 1+i |
3.已知函数f(x)=sin(2ωx一$\frac{π}{4}$)(ω>0)的最小正周期为π,则函数f(x)的图象( )
| A. | 关于点($\frac{π}{8}$,0)对称 | B. | 关于直线x=$\frac{π}{8}$对称 | ||
| C. | 关于点(-$\frac{π}{4}$,0)对称 | D. | 关于直线x=-$\frac{π}{4}$对称 |
13.设复数z满足(1+i)z=2,则z的共轭复数$\overline{z}$=( )
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
18.若命题:“?x∈R,x2-2ax+a≤0”为假命题,则$\frac{{2{a^2}+1}}{a}$的最小值是( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
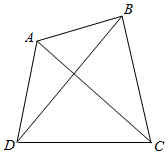 为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.
为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.