题目内容
15.定义$\overline{abc}$是一个三位数,其中各数位上的数字a,b,c∈{0,1,2,3,4,5,6,7,8,9}且不全相同,定义如下运算f:把$\overline{abc}$的三个数字a,b,c自左到右分别由大到小排列和由小到大排列(若非零数字不足三位则在前面补0),然后用“较大数”减去“较小数”,例如:f(100)=100-001-099,f(102)=210-0.12-198,如下定义一个三位数序列:第一次实施运算f的结果记为$\overline{{a}_{1}{b}_{1}{c}_{1}}$,对于n>1且n∈N,$\overline{{a}_{n}{b}_{n}{c}_{n}}=f(\overline{{a}_{n-1}{b}_{n-1}{c}_{n-1}})$,将$\overline{{a}_{n}{b}_{n}{c}_{n}}$的三个数字中的最大数字与最小数字的差记为dn(Ⅰ)当$\overline{abc}$=636时,求$\overline{{a}_{1}{b}_{1}{c}_{1}}$,$\overline{{a}_{2}{b}_{2}{c}_{2}}$及d2的值;
(Ⅱ)若d1=6,求证:当n>1时,dn=5;
(Ⅲ)求证:对任意三位数$\overline{abc}$,n≥6时,$\overline{{a}_{n}{b}_{n}{c}_{n}}$=495.
分析 (Ⅰ)利用新定义之间通过$\overline{abc}$=636时,求解$\overline{{a}_{1}{b}_{1}{c}_{1}}$,$\overline{{a}_{2}{b}_{2}{c}_{2}}$及d2的值;
(Ⅱ)不妨设,an≥bn≥cn,推出f($\overline{{a}_{n}{b}_{n}{c}_{n}}$)=dn×99,若d1=6,得到$\overline{{a}_{2}{b}_{2}{c}_{2}}$=f($\overline{{a}_{1}{b}_{1}{c}_{1}}$)=6×99=495,可得d2=5,然后利用数学归纳法证明当n>1时,dn=5;
(Ⅲ)数字a,b,c∈{0,1,2,3,4,5,6,7,8,9}且不全相同,三个数字中的最大数字与最小数字的差记为d,推出d1=$\left\{\begin{array}{l}{10-d,d≤5}\\{d-1,d>5}\end{array}\right.$,dn+1=$\left\{\begin{array}{l}{10-{d}_{n},{d}_{n}≤5}\\{{d}_{n}-1,{d}_{n}>5}\end{array}\right.$,dn∈{5,6,7,8,9},证明对任意三位数$\overline{abc}$,n≥6时,$\overline{{a}_{n}{b}_{n}{c}_{n}}$=495.
解答 解:(Ⅰ)当$\overline{abc}$=636时,$\overline{{a}_{1}{b}_{1}{c}_{1}}$=663-366-297,
$\overline{{a}_{2}{b}_{2}{c}_{2}}$=972-279-693
d2=6;
(Ⅱ)不妨设,an≥bn≥cn,则f($\overline{{a}_{n}{b}_{n}{c}_{n}}$)=(an×100+bn×10+cn)-(cn×100+bn×10+an)=(an-cn)×99=dn×99,若d1=6,则$\overline{{a}_{2}{b}_{2}{c}_{2}}$=f($\overline{{a}_{1}{b}_{1}{c}_{1}}$)=6×99=495,可得d2=9-4=5,
所以n=2时成立,假设n=k(k>1)时成立,即dk=5,
则$\overline{{a}_{k+1}{b}_{k+1}{c}_{k+1}}$=f($\overline{{a}_{n}{b}_{n}{c}_{n}}$)=dk×99=495,dk+1=9-4=5.
综上:当n>1时,dn=5;
(Ⅲ)数字a,b,c∈{0,1,2,3,4,5,6,7,8,9}且不全相同,三个数字中的最大数字与最小数字的差记为d,
则d∈{1,2,3,4,5,6,7,8,9},$\overline{{a}_{1}{b}_{1}{c}_{1}}$=f($\overline{abc}$)=$d×99=100d-d=\overline{d00}-\overline{00d}$,所以a1=d-1,b1=9,c1=10-d,所以d1=$\left\{\begin{array}{l}{10-d,d≤5}\\{d-1,d>5}\end{array}\right.$,所以d1∈{5,6,7,8,9},
同理:$\overline{{a}_{n+1}{b}_{n+1}{c}_{n+1}}$=f($\overline{{a}_{n}{b}_{n}{c}_{n}}$)=dk×99=$\overline{{d}_{n}00}-\overline{00{d}_{n}}$,所以an+1=dn-1,bn+1=9,cn+1=10-dn,
所以dn+1=$\left\{\begin{array}{l}{10-{d}_{n},{d}_{n}≤5}\\{{d}_{n}-1,{d}_{n}>5}\end{array}\right.$,dn∈{5,6,7,8,9},
当n≤5时,dn=5,所以n≥6时,n≥6时,$\overline{{a}_{n}{b}_{n}{c}_{n}}$=dn+1×99=5×99=495.
点评 本题考查归纳推理,数学归纳法的应用,数列与函数的关系,考查分析问题解决问题的能力.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案| A. | 36 | B. | 27 | C. | 54 | D. | 45 |
| A. | {x|2<x<3} | B. | {x|-2<x<0} | C. | {x|0<x<2} | D. | {x|-2<x<3} |
| A. | 关于点($\frac{π}{8}$,0)对称 | B. | 关于直线x=$\frac{π}{8}$对称 | ||
| C. | 关于点(-$\frac{π}{4}$,0)对称 | D. | 关于直线x=-$\frac{π}{4}$对称 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
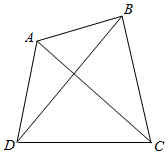 为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.
为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.