题目内容
11.已知a>0,${(\frac{a}{{\sqrt{x}}}-x)^6}$展开式的常数项为15,则$\int_{-a}^a{({x^2}+x+\sqrt{4-{x^2}}})dx$=$\frac{2}{3}+\frac{2π}{3}+\sqrt{3}$.分析 由条件利用二项式展开式的通项公式求得a的值,再利用积分的运算性质、法则,求得要求式子的值.
解答 解:由${(\frac{a}{{\sqrt{x}}}-x)^6}$的展开式的通项公式为Tr+1=${C}_{6}^{r}$•(-1)r•a6-r•${x}^{\frac{3r-6}{2}}$,
令$\frac{3r-6}{2}$=0,求得r=2,故常数项为$C_6^4{a^4}=15$,可得a=1,
因此原式为$\int_{-1}^1{({x^2}+x+\sqrt{4-{x^2}})}dx=2\int_0^1{({x^2}+\sqrt{4-{x^2}})}dx=2(\int_0^1{x^2}dx+\int_0^1{\sqrt{4-{x^2}}}dx)$
=$2(\frac{1}{3}+\frac{{π•{2^2}}}{12}+\frac{1}{2}×1×\sqrt{3})=\frac{2}{3}+\frac{2π}{3}+\sqrt{3}$,
故答案为:$\frac{2}{3}+\frac{2π}{3}+\sqrt{3}$.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,积分的运算,是一道中档的常规问题

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
1. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{13}$ |
2.“吸烟有害健康,吸烟会对身体造成伤害”,哈尔滨市于2012年5月31日规定室内场所禁止吸烟.美国癌症协会研究表明,开始吸烟年龄(X)分别为16岁、18岁、20岁和22岁,其得肺癌的相对危险度(Y)依次为15.10、12.81、9.72、3.21;每天吸烟(U)10支、20支、30支者,其得肺癌的相对危险度(v)分别为7.5、9.5和16.6.用r1表示变量X与y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
| A. | rl=r2 | B. | r1>r2>0 | C. | 0<r1<r2 | D. | r1<0<r2 |
19.已知复数z满足z(1+i)=1(i为虚数单位),则z=( )
| A. | $\frac{1-i}{2}$ | B. | $\frac{1+i}{2}$ | C. | 1-i | D. | 1+i |
6.设集合A={x|x2-3x<0},B={x||x|<2},则A∩B=( )
| A. | {x|2<x<3} | B. | {x|-2<x<0} | C. | {x|0<x<2} | D. | {x|-2<x<3} |
3.已知函数f(x)=sin(2ωx一$\frac{π}{4}$)(ω>0)的最小正周期为π,则函数f(x)的图象( )
| A. | 关于点($\frac{π}{8}$,0)对称 | B. | 关于直线x=$\frac{π}{8}$对称 | ||
| C. | 关于点(-$\frac{π}{4}$,0)对称 | D. | 关于直线x=-$\frac{π}{4}$对称 |
1.已知i是虚数单位,若复数z满足z=$\frac{{i}^{3}}{1+i}$,则z为( )
| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{-1-i}{2}$ | D. | $\frac{-1+i}{2}$ |
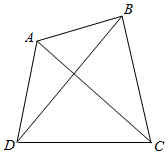 为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.
为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.