题目内容
18.某公司为了解下属某部门对企业职工的服务情况,随机访问50名职工.根据这50名职工对该部门的评分,得到的频率分布表如下:| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.1 |
| [60,70) | m | 0.2 |
| [70,80) | 15 | n |
| [80,90) | 12 | 0.24 |
| 8 | 0.16 | |
| 合计 | 50 | 1 |
(Ⅱ)同一组中的数据用区间的中点值作代表,求这50名职工对该部门的评分的平均分.
分析 (Ⅰ)由频率分布表中求出m、n位置的相应数据即可,并画出频率分布直方图,
(Ⅱ)根据平均数的定义即可求出.
解答  解:(Ⅰ)频率分布表如下:
解:(Ⅰ)频率分布表如下:
m=50-(5+15+12+8)=10,
$n=\frac{15}{50}=0.3$,
频率分布直方图如图所示:
(Ⅱ)$\overline x$=55×0.1+65×0.2+75×0.3+85×0.24+95×0.16
=76.6.
点评 本题考查频率分布直方图的应用,平均数的求法,是基础题.

练习册系列答案
相关题目
8.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{169}$=1的焦点坐标为( )
| A. | (5,0),(-5,0) | B. | (0,5),(0,-5) | C. | (0,12),(0,-12) | D. | (12,0),(-12,0) |
3.某班5名学生的数学和物理成绩如表:
(1)画出散点图;
(2)求物理成绩y对数学成绩x的线性回归方程:
(3)一名学生的数学成绩为96分,试预测他的物理成绩.
参考数据:$\sum_{i=1}^5{{x_i}{y_i}}=25054,\sum_{i=1}^5{{x_i}^2}=27174$.
| 学生 学科 | A | B | C | D | E |
| 数学成绩(x) | 88 | 76 | 73 | 66 | 63 |
| 物理成绩(y) | 78 | 65 | 71 | 64 | 61 |
(2)求物理成绩y对数学成绩x的线性回归方程:
(3)一名学生的数学成绩为96分,试预测他的物理成绩.
参考数据:$\sum_{i=1}^5{{x_i}{y_i}}=25054,\sum_{i=1}^5{{x_i}^2}=27174$.
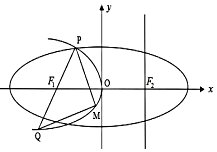 如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.
如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动. 如图所示,某幼儿园有一个游乐场ABCD,其中AB=50米,BC=40米,由于幼儿园招生规模增大,需将该游乐场扩大成矩形区域EFGH,要求A、B、C、D四个点分别在矩形EFGH的四条边(不含顶点)上.设∠BAE=θ(弧度),EF的长为y米.
如图所示,某幼儿园有一个游乐场ABCD,其中AB=50米,BC=40米,由于幼儿园招生规模增大,需将该游乐场扩大成矩形区域EFGH,要求A、B、C、D四个点分别在矩形EFGH的四条边(不含顶点)上.设∠BAE=θ(弧度),EF的长为y米.