题目内容
13.设函数f(x)=sinωx+$\sqrt{3}$cosωx(ω>0)的周期为π.(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)说明函数f(x)的图象可由y=sinx的图象经过怎样的变换而得到.
分析 (Ⅰ)通过两角和与差的三角函数化简函数的解析式,通过三角函数的周期求解ω,利用正弦函数的单调增区间求解即可
(Ⅱ)法一:把y=sinx的图象向左平移$\frac{π}{3}$个单位,然后再把函数图象上的点的横坐标缩短到原来的$\frac{1}{2}$,把函数的图象上的点的纵坐标伸长到原来的2倍(横坐标不变推出结果;
法二:把y=sinx的图象上的点的横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),然后再将所得函数的图象向左平移$\frac{π}{6}$个单位,在把图象上的点的纵坐标伸长到原来的2倍(横坐标不变),求出结果即可.
解答 解:(Ⅰ)$f(x)=sinωx+\sqrt{3}cosωx$=$2(\frac{1}{2}sinωx+\frac{{\sqrt{3}}}{2}cosωx)$=$2sin(ωx+\frac{π}{3})$∴$T=\frac{2π}{ω}=π$,即ω=2,
∴$f(x)=2sin(2x+\frac{π}{3})$…3分
∵$2kπ-\frac{π}{2}≤2x+\frac{π}{3}≤2kπ+\frac{π}{2}$,k∈Z∴$kπ-\frac{5π}{12}≤x≤kπ+\frac{π}{12}$
故f(x)的单调递增区间:$[kπ-\frac{5π}{12},kπ+\frac{π}{12}]$k∈Z…5分
(Ⅱ)法一:把y=sinx的图象向左平移$\frac{π}{3}$个单位,得到$y=sin(x+\frac{π}{3})$的图象;
再把$y=sin(x+\frac{π}{3})$的图象上的点的横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),得到$y=sin(2x+\frac{π}{3})$的图象;
最后把$y=sin(2x+\frac{π}{3})$的图象上的点的纵坐标伸长到原来的2倍(横坐标不变),即可得到$f(x)=2sin(2x+\frac{π}{3})$的图象. …9分(不对酌情给分)
法二:把y=sinx的图象上的点的横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),得到y=sin2x的图象;
再将y=sin2x的图象向左平移$\frac{π}{6}$个单位,得到$y=sin(2x+\frac{π}{3})$的图象;
最后把$y=sin(2x+\frac{π}{3})$的图象上的点的纵坐标伸长到原来的2倍(横坐标不变),即可得到$f(x)=2sin(2x+\frac{π}{3})$的图象.…9分(不对酌情给分)
点评 本题考查三角函数的图形的变换,正弦函数的单调性的求法,考查转化思想以及计算能力.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | 函数f(x)的最小正周期为$\frac{π}{3}$ | |
| B. | 函数f(x)的图象关于点$({\frac{7π}{9},0})$对称 | |
| C. | 函数f(x)在区间$({\frac{π}{4},\frac{11π}{24}})$上是增函数 | |
| D. | 由y=2cos2x的图象向右平移$\frac{5π}{12}$个单位长度可以得到函数f(x)的图象 |
| A. | y=tan3x | B. | y=cosx | C. | y=2sinx-1 | D. | y=2x |
| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.1 |
| [60,70) | m | 0.2 |
| [70,80) | 15 | n |
| [80,90) | 12 | 0.24 |
| 8 | 0.16 | |
| 合计 | 50 | 1 |
(Ⅱ)同一组中的数据用区间的中点值作代表,求这50名职工对该部门的评分的平均分.
| A. | 3 | B. | 1 | C. | 0 | D. | 2 |
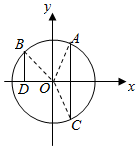 (理) 如图,在平面直角坐标系xoy中,点A(x1,y1),B(x2,y2)在单位圆上,∠xOA=α,$α∈(\frac{π}{6},\frac{π}{2})$,$∠AOB=\frac{π}{3}$.
(理) 如图,在平面直角坐标系xoy中,点A(x1,y1),B(x2,y2)在单位圆上,∠xOA=α,$α∈(\frac{π}{6},\frac{π}{2})$,$∠AOB=\frac{π}{3}$.