题目内容
 如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上;如果∠P=50°,那么∠ACB等于
如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上;如果∠P=50°,那么∠ACB等于考点:弦切角
专题:立体几何
分析:利用切线长定理和弦切角定理即可得出.
解答:
解:∵PA、PB是⊙O的切线,
∴∠PAB=∠PBA.
∵∠P=50°,∴∠PAB=
(180°-50°)=65°.
由弦切角定理可得:∠C=∠PAB=65°.
故答案为:65°.
∴∠PAB=∠PBA.
∵∠P=50°,∴∠PAB=
| 1 |
| 2 |
由弦切角定理可得:∠C=∠PAB=65°.
故答案为:65°.
点评:本题考查了切线长定理和弦切角定理、三角形的内角和定理,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
已知p、q是两个命题,若“(¬p)∨q”是假命题,则( )
| A、p、q都是假命题 |
| B、p、q都是真命题 |
| C、p是假命题q是真命题 |
| D、p是真命题q是假命题 |
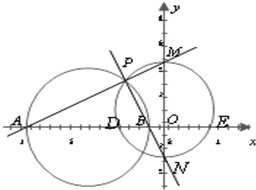 如图,已知圆C直径的两个端点坐标分别为A(-9,0)、B(-1,0),点P为圆C上(不同于A、B)的任意一点,连接AP、BP分别交y轴于M、N两点,以MN为直径的圆与x轴交于D、F两点,则弦长|DF|为( )
如图,已知圆C直径的两个端点坐标分别为A(-9,0)、B(-1,0),点P为圆C上(不同于A、B)的任意一点,连接AP、BP分别交y轴于M、N两点,以MN为直径的圆与x轴交于D、F两点,则弦长|DF|为( )| A、7 | ||
| B、6 | ||
C、2
| ||
D、2
|
一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为( )厘米.
| A、9 | B、10 | C、11 | D、12 |
已知一个正三棱锥的三条侧棱两两垂直且相等,底面边长为2,则该三棱锥的外接球的表面积是( )
| A、6π | B、12π |
| C、18π | D、24π |