题目内容
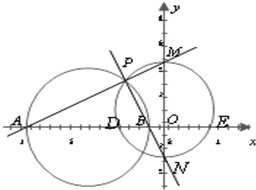 如图,已知圆C直径的两个端点坐标分别为A(-9,0)、B(-1,0),点P为圆C上(不同于A、B)的任意一点,连接AP、BP分别交y轴于M、N两点,以MN为直径的圆与x轴交于D、F两点,则弦长|DF|为( )
如图,已知圆C直径的两个端点坐标分别为A(-9,0)、B(-1,0),点P为圆C上(不同于A、B)的任意一点,连接AP、BP分别交y轴于M、N两点,以MN为直径的圆与x轴交于D、F两点,则弦长|DF|为( )| A、7 | ||
| B、6 | ||
C、2
| ||
D、2
|
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:求出以A(-9,0)、B(-1,0)为直径的圆的方程,可得P的坐标,求出直线PA,PB的方程,可得M,N的坐标,进而可得MN的中点坐标,以MN为直径的圆的半径,利用弦长公式,即可得出结论.
解答:
解:以A(-9,0)、B(-1,0)为直径的圆的方程为(x+5)2+y2=16,则P(-5+4cosα,4sinα),
∴PA:y=
•(x+9),PB:y=
•(x+1),
令x=0,可得M(0,
),N(0,
),
∴MN的中点坐标为(0,
),以MN为直径的圆的半径为
,
∴|DF|=2
=6.
故选B.
∴PA:y=
| sinα |
| cosα+1 |
| sinα |
| cosα-1 |
令x=0,可得M(0,
| 9sinα |
| cosα+1 |
| sinα |
| cosα-1 |
∴MN的中点坐标为(0,
| 5cosα-4 |
| sinα |
| 5-4cosα |
| sinα |
∴|DF|=2
(
|
故选B.
点评:本题考查圆的方程,考查直线方程,考查直线与圆的位置关系,考查弦长公式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个几何体的三视图如图所示,则这个几何体的体积为( )


A、6
| ||
| B、9 | ||
C、18
| ||
| D、27 |
已知函数y=ax-1-1(a>0切a≠1)的图象恒过点P,角α的终边过点P,则sinα=( )
A、-
| ||||
| B、1 | ||||
C、
| ||||
| D、0 |
在空间直角坐标系中,点P(3,4,5)关于xOy平面的对称点的坐标是( )
| A、(-3,4,5) |
| B、(-3,-4,5) |
| C、(3,4,-5) |
| D、(-2,-4,-5) |
一元二次不等式x2-7x+12<0,2x2+x-5>0,x2+2>-2x的解集分别是M、N、P,则M、N、P之间的包含关系是( )
| A、N⊆M⊆P |
| B、M⊆N⊆P |
| C、N⊆P⊆M |
| D、M⊆P⊆N |
 如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上;如果∠P=50°,那么∠ACB等于
如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上;如果∠P=50°,那么∠ACB等于