题目内容
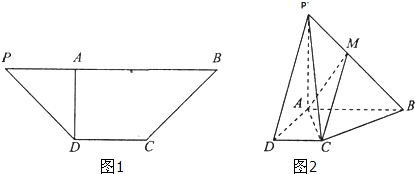
如图,在等腰梯形PDCB中,DC∥PB,PB=3DC=3,PD=
,DA⊥PB,垂足为A,将△PAD沿AD折起到点P′,使得P′A⊥AB,得到四棱锥P′-ABCD,点M在棱P′B上.
(Ⅰ)证明:平面P′AD⊥平面P′CD;
(Ⅱ)平面AMC把四棱锥P′-ABCD分成两个几何体,当P′D∥平面AMC时,求这两个几何体的体积之比
的值.
| 2 |
(Ⅰ)证明:平面P′AD⊥平面P′CD;
(Ⅱ)平面AMC把四棱锥P′-ABCD分成两个几何体,当P′D∥平面AMC时,求这两个几何体的体积之比
| VP′M-ACD |
| VM-ABC |

考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)由图1中DA⊥P′B,可得折叠后DA⊥AB,DA⊥P′A,进而DC⊥P′A,DC⊥DA,由线面垂直的判定定理得到DC⊥平面P′AD,再由面面垂直的判定定理得到平面P′AD⊥平面P′CD;
(2)根据几何图形可知
=
,求出四棱锥P′-ABCD的高为h,底面积为
×(1+2)×1=
,三棱锥M-ABC的高为h0,底面积为
×2×1=1,
=
,利用分割法求解体积,得出比值,
(2)根据几何图形可知
| P′M |
| MB |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| h0 |
| h |
| 2 |
| 3 |
解答:
 证明:(1)因为在图a的等腰梯形PDCB中,DA⊥PB,
证明:(1)因为在图a的等腰梯形PDCB中,DA⊥PB,
所以在四棱锥P′-ABCD中,DA⊥AB,DA⊥P′A
又P′A⊥AB,且DC∥AB,所以DC⊥P′A,DC⊥DA,
而DA?平面P′AD,P′A?平面P′AD,P′A∩DA=A,
所以DC⊥平面P′AD
因为DC?平面P′CD,
所以平面P′AD⊥平面P′CD,
解:(2)∵在等腰梯形PDCB中,DC∥PB,PB=3DC=3,PD=
,
∴AD=1,BD=
,BD与AC的交点为O,
可得OD=
,OB=
,
∵当P′D∥平面AMC时,
∴P′D∥0M,
∴
=
,
∵根据体积公式:
sh,
∴三棱锥M-ABC与四棱锥P′-ABCD的体积之比为
,
这两个几何体的体积之比
=
=
 证明:(1)因为在图a的等腰梯形PDCB中,DA⊥PB,
证明:(1)因为在图a的等腰梯形PDCB中,DA⊥PB,所以在四棱锥P′-ABCD中,DA⊥AB,DA⊥P′A
又P′A⊥AB,且DC∥AB,所以DC⊥P′A,DC⊥DA,
而DA?平面P′AD,P′A?平面P′AD,P′A∩DA=A,
所以DC⊥平面P′AD
因为DC?平面P′CD,
所以平面P′AD⊥平面P′CD,
解:(2)∵在等腰梯形PDCB中,DC∥PB,PB=3DC=3,PD=
| 2 |
∴AD=1,BD=
| 5 |
可得OD=
| ||
| 3 |
2
| ||
| 3 |
∵当P′D∥平面AMC时,
∴P′D∥0M,
∴
| h0 |
| h |
| 2 |
| 3 |
∵根据体积公式:
| 1 |
| 3 |
∴三棱锥M-ABC与四棱锥P′-ABCD的体积之比为
| 4 |
| 9 |
这两个几何体的体积之比
| VP′M-ACD |
| VM-ABC |
| ||
1-
|
| 4 |
| 5 |
点评:本题考察了空间几何体的性质,运用求解体积,面积,线段的长,分割法求解几何体的体积,属于难题.

练习册系列答案
相关题目
 某车间共有6名工人,他们某日加工零件葛素的茎叶图如图所示,其中茎为十位数,叶为个位数日加工零件大于样本均值的工人为优秀工人,从该车间6名工人中,任取2人,则恰由1名优秀工人的概率为( )
某车间共有6名工人,他们某日加工零件葛素的茎叶图如图所示,其中茎为十位数,叶为个位数日加工零件大于样本均值的工人为优秀工人,从该车间6名工人中,任取2人,则恰由1名优秀工人的概率为( )