Question

已知直线系l的方程xcosθ+（y-2）sinθ=1（其中θ是常数，且0≤θ≤2π），若该直线系所围成的集合图形为M．
（1）试用代数式表示图形M；
（2）若点（x，y）在M中，试求

y+1

x+2

的取值范围．

Answer 1

考点：简单线性规划的应用

专题：计算题,作图题,函数的性质及应用

分析：（1）由题意，点（0，2）到直线xcosθ+（y-2）sinθ=1的距离d=1，则直线系所围成的几何图形为M为圆；
（2）由题意，设

y+1

x+2

=k，则y=k（x+2）-1与圆的方程x²+（y-2）²=1联立有解即可．

解答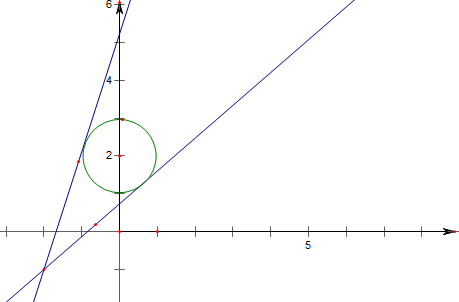： 解：（1）由xcosθ+（y-2）sinθ=1知，
点（0，2）到直线xcosθ+（y-2）sinθ=1的距离d=1，
则图形M为x²+（y-2）²=1；
（2）设

y+1

x+2

=k，则y=k（x+2）-1，
与圆的方程x²+（y-2）²=1联立消去y得，
x²+（k（x+2）-3）²=1，
即（k²+1）x²+（4k²-6k）x+4k²-12k+8=0，
则△=（4k²-6k）²-4（k²+1）（4k²-12k+8）≥0，
即3k²-12k+8≤0，
则

6-2 3

3

≤k≤

6+2 3

3

．
即

6-2 3

3

≤

y+1

x+2

≤

6+2 3

3

．

点评：本题考查了对几何图形与代数式关系的认识，同时考查了直线与圆的位置关系问题，属于中档题．