题目内容
已知P为⊙B：（x+2）2+y2=36上一动点，点A（2，0），线段AP垂直平分线交直线BP于点Q，求点Q的轨迹方程．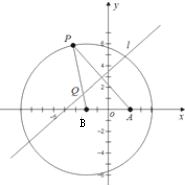
考点：椭圆的定义
专题：圆锥曲线的定义、性质与方程
分析：结合已知条件根据椭圆的定义，点Q的轨迹是中心在原点，以B、A为焦点，长轴长等于6的椭圆，由此能求出点Q的轨迹方程．
解答：
解：（1）圆C的圆心为B（-2，0），半径r=6，|BA|=4．
连结QA，由已知得|QA|=|QP|，
∵|QB|+|QA|=|QB|+|QP|=BP=r=6＞|BA|．
根据椭圆的定义，点Q的轨迹是中心在原点，以B、A为焦点，长轴长等于6的椭圆，
即a=3，c=2，b2=a2-c2=9-4=5，
∴点Q的轨迹方程为
+
=1．
连结QA，由已知得|QA|=|QP|，
∵|QB|+|QA|=|QB|+|QP|=BP=r=6＞|BA|．
根据椭圆的定义，点Q的轨迹是中心在原点，以B、A为焦点，长轴长等于6的椭圆，
即a=3，c=2，b2=a2-c2=9-4=5，
∴点Q的轨迹方程为
| x2 |
| 9 |
| y2 |
| 5 |
点评：本题考查点的轨迹方程的求法，解题时要认真审题．
练习册系列答案
小学教材完全解读系列答案
相关题目
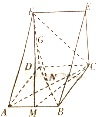已知直三棱柱BCE-ADG，底面△ADF中，AD⊥DF，DA=DF=DC，其中M，N分别是AB，AC的中点，G是DF上的一个动点．