题目内容

设向量
a
，
b
满足|
a
+
b
|=
6
，|
a
|=1，|
b
|=2，则
a
•
b
等于（　　）
A、
1
5
B、
1
4
C、
1
3
D、
1
2
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由条件把|
a
+
b
|=
6
平方，可得
a
•
b
的值．
解答： 解：∴向量
a
，
b
满足|
a
+
b
|=
6
，|
a
|=1，|
b
|=2，∴
a
2+
b
2+2
a
•
b
=6，即 1+4+2
a
•
b
=6，
求得
a
•
b
=
1
2
，
故选：D．
点评：本题主要考查两个向量的数量积公式，求向量的模的方法，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
1+a•2x
2x+1
是奇函数，
（1）求实数a的值
（2）判断函数f（x）在R上的单调性，并用定义加以证明．
下列各组函数f（x）与g（x）的图象相同的是（　　）
A、f（x）=x，g（x）=（
x
）2
B、f（x）=x2，g（x）=（x+1）2
C、f（x）=1，g（x）=
x
x
D、f（x）=|x|，g（x）=
x
-x
(x≥0)
(x＜0)
在直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知圆C的圆心的极坐标为（
2
，
π
4
），半径r=
2
，点P的极坐标为（2，π），过P作直线l交圆C于A，B两点．
（1）求圆C的直角坐标方程；
（2）求|PA|•|PB|的值．
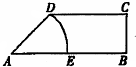一只受伤的丹顶鹤在如图所示（直角梯形）的草原上飞过，其中AD=
2
，DC=2，BC=1，它可能随机在草原上任何一处（点），若落在扇形沼泽区域ADE以外丹顶鹤能生还，则该丹顶鹤生还的概率是（　　）
A、
1
2
-
π
15
B、1-
π
10
C、1-
π
6
D、1-
3π
10
已知点P（x，y）的坐标满足
x+y-4≤0
1≤x≤2
y≥0
，则z=x+2y的最大值为
 
．
已知函数f（x）=
a
3
x3+ax2+cx，g(x)=ax2+2ax+c，a≠0，则它们的图象可能是（　　）
A、
B、
C、
D、
已知P（2，-1），过P点且与原点距离最大的直线的方程是（　　）
A、x-2y-5=0
B、2x-y-5=0
C、x+2y-5=0
D、2x+y+5=0
集合A={富强，民主，文明，和谐}，B={自由，平等，公正，法治}，C={爱国，敬业，诚信，友善}，则集合（A∪B）∩C的真子集的个数是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网