Question

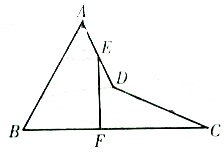如图，在空间四边形ABCD中，两条对边AB=CD=3，E、F分别是另外两条对边AD，BC上的点，

AE

ED

=

BF

FC

=

1

2

，EF=

5

，求AB和CD所成角的大小．

Answer 1

考点：异面直线及其所成的角

专题：计算题,空间位置关系与距离

分析：在BD上取靠近B的三等分点G，连接FG、GE，可证∠EGF或其补角就是异面直线AB和CD所成角，在△EFG中由勾股定理的逆定理可得∠EGF=90°，可得答案．

解答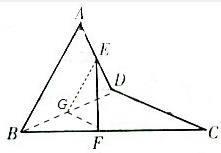： 解：（如图）在BD上取靠近B的三等分点G，连接FG、GE，
在△BCD中，可得

BG

GD

=

BF

FC

，故有FG∥DC，
同理在△ABD中，可得GE∥AB，
所以∠EGF或其补角就是异面直线AB和CD所成角，
在△BCD中，由GE∥CD，CD=3，

FG

CD

=

1

3

，得FG=1，
在△ABD中，由EG∥AB，AB=3，

EG

AB

=

2

3

，得EG=2，
在△EFG中，由EG=2，FG=1，EF=

5

，则EG²+FG²=EF²，
由勾股定理的逆定理，可得∠EGF=90°，
所以异面直线AB和CD所成角为90°

点评：本题考查异面直线所成的角的求法，涉及勾股定理的逆定理的应用，属中档题．