题目内容
已知抛物线y2=6x.
(1)求以点M(4,1)为中点的弦所在的直线方程;
(2)求过焦点F的弦的中点轨迹;
(3)求抛物线被直线y=x-b所截得的弦的中点的轨迹方程.
(1)求以点M(4,1)为中点的弦所在的直线方程;
(2)求过焦点F的弦的中点轨迹;
(3)求抛物线被直线y=x-b所截得的弦的中点的轨迹方程.
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:(1)设所求直线与抛物线相交于点A(x1,y1),B(x2,y2).可得
=6x1,
=6x2,两方程相减可得
=6,利用中点坐标公式、斜率计算公式即可得出kAB,利用点斜式即可.
(2)抛物线y2=6x的焦点F(
,0).设所求直线的方程为my=x-
,与抛物线相交于两点C(x3,y3),D(x4,y4),线段CD的中点N(x0,y0).与抛物线的方程联立可得根与系数的关系,利用中点坐标公式并消去参数m即可得出.
(3)设直线y=x-b与抛物线相交于两点E(x5,y5),F(x6,y6),线段EF的中点Q(x,y).与抛物线方程联立,化为y2-6y-6b=0,△>0,解得b>-
.再利用中点坐标公式即可得出.
| y | 2 1 |
| y | 2 2 |
| (y1+y2)(y1-y2) |
| x1-x2 |
(2)抛物线y2=6x的焦点F(
| 3 |
| 2 |
| 3 |
| 2 |
(3)设直线y=x-b与抛物线相交于两点E(x5,y5),F(x6,y6),线段EF的中点Q(x,y).与抛物线方程联立,化为y2-6y-6b=0,△>0,解得b>-
| 3 |
| 2 |
解答:
解:(1)设所求直线与抛物线相交于点A(x1,y1),B(x2,y2).
则
=6x1,
=6x2,
∴
=6,
∴2kAB=6,
∴kAB=3.
∴以点M(4,1)为中点的弦所在的直线方程是y-1=3(x-4),化为3x-y-11=0.
(2)抛物线y2=6x的焦点F(
,0).
设所求直线的方程为my=x-
,与抛物线相交于两点C(x3,y3),D(x4,y4),线段CD的中点N(x0,y0).
联立
,化为y2-6my-9=0.
△>0.
∴y3+y4=6m=2y0,∴y0=3m.
∴x0=my0+
=
+
.
化为
=3(x0-
)(x0≥
),即为过焦点F的弦的中点轨迹方程.
(3)设直线y=x-b与抛物线相交于两点E(x5,y5),F(x6,y6),线段EF的中点Q(x,y).
联立
,化为y2-6y-6b=0,△=36+24b>0,
解得b>-
.
y5+y6=6=2y,∴y=3,x=3+b(b>-
).
抛物线被直线y=x-b所截得的弦的中点的轨迹方程为y=3,x=3+b(b>-
).
则
| y | 2 1 |
| y | 2 2 |
∴
| (y1+y2)(y1-y2) |
| x1-x2 |
∴2kAB=6,
∴kAB=3.
∴以点M(4,1)为中点的弦所在的直线方程是y-1=3(x-4),化为3x-y-11=0.
(2)抛物线y2=6x的焦点F(
| 3 |
| 2 |
设所求直线的方程为my=x-
| 3 |
| 2 |
联立
|
△>0.
∴y3+y4=6m=2y0,∴y0=3m.
∴x0=my0+
| 3 |
| 2 |
| ||
| 3 |
| 3 |
| 2 |
化为
| y | 2 0 |
| 3 |
| 2 |
| 3 |
| 2 |
(3)设直线y=x-b与抛物线相交于两点E(x5,y5),F(x6,y6),线段EF的中点Q(x,y).
联立
|
解得b>-
| 3 |
| 2 |
y5+y6=6=2y,∴y=3,x=3+b(b>-
| 3 |
| 2 |
抛物线被直线y=x-b所截得的弦的中点的轨迹方程为y=3,x=3+b(b>-
| 3 |
| 2 |
点评:本题考查了直线与抛物线相交弦的中点轨迹问题转化为方程联立、根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知f(x)=2cos
x,则f(0)+f(1)+f(2)+…+f(2008)=( )
| π |
| 6 |
| A、1 | ||
B、3+
| ||
C、2+
| ||
| D、0 |
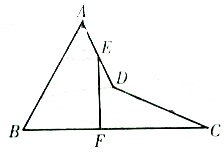 如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点,
如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点, 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EP⊥PB交PB于点F
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EP⊥PB交PB于点F 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的体积是( )
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的体积是( )