题目内容
已知等差数列{an}的前项和为Sn,且a3=5,S15=225.
(1)求数列{an}的通项an;
(2)设bn=an+1-
,求数列{bn}的前项和Tn.
(1)求数列{an}的通项an;
(2)设bn=an+1-
| n |
| 2n-1 |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)根据等差数列的通项公式、前n项和公式列出方程组,求出首项a1、公差d,再求出通项an;
(Ⅱ)由(Ⅰ)先求出bn,根据bn的特点利用分组求和、错位相减法求出前项和Tn.
(Ⅱ)由(Ⅰ)先求出bn,根据bn的特点利用分组求和、错位相减法求出前项和Tn.
解答:
解:(Ⅰ)设等差数列{an}首项为a1,公差为d,
由题意得,
,解得
所以an=1+2(n-1)=2n-1;
(II)由(I)知,bn=an+1-
=2n-
,
所以Tn=2(1+2+…+n)-(
+
+
+…+
),
设s=
+
+
+…+
,①
s=
+
+
+…+
,②
①-②得,
s=1+
+
+
+…+
-
=1+
-
=2-
,则s=4-
,
所以Tn=2×
-(4-
)=n(n+1)+
-4.
由题意得,
|
|
所以an=1+2(n-1)=2n-1;
(II)由(I)知,bn=an+1-
| n |
| 2n-1 |
| n |
| 2n-1 |
所以Tn=2(1+2+…+n)-(
| 1 |
| 20 |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
设s=
| 1 |
| 20 |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 21 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
①-②得,
| 1 |
| 2 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
| n |
| 2n |
=1+
| ||||
1-
|
| n |
| 2n |
| n+2 |
| 2n |
| n+2 |
| 2n-1 |
所以Tn=2×
| n(n+1) |
| 2 |
| n+2 |
| 2n-1 |
| n+2 |
| 2n-1 |
点评:本题等差数列的通项公式、前n项和公式,以及数列求和方法:错位相减法和分组求和,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
不等式|
|<x的解集是( )
| x+1 |
| x-1 |
| A、{x|0x<1}∪{x|x>1} | ||||
B、{x|1-
| ||||
| C、{x|-1x<0} | ||||
D、{x|x>1+
|
若函数f(x)=
,若a•f(-a)<0,则实数a的取值范围是( )
|
| A、(-1,0)∪(1,+∞) |
| B、(-∞,-1)∪(0,1) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-1,0)∪(0,1) |
如果椭圆方程是
+
=1,那么焦距是( )
| x2 |
| 16 |
| y2 |
| 12 |
| A、2 | ||
B、2
| ||
| C、4 | ||
| D、8 |
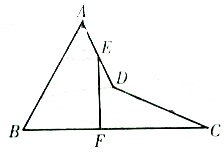 如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点,
如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点, 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的体积是( )
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的体积是( )