题目内容
给出下列说法:
(1)函数y=
和y=x
是同一个函数;
(2)f(x)=
(x∈[2,6])的值域为(
,2);
(3)既奇又偶的函数只有f(x)=0;
(4)集合{x∈
=
,a∈N*}中只有四个元素;
其中正确的命题有 (只写序号).
(1)函数y=
| -2x3 |
| -2x |
(2)f(x)=
| 2 |
| x-1 |
| 2 |
| 5 |
(3)既奇又偶的函数只有f(x)=0;
(4)集合{x∈
| N |
| x |
| 6 |
| a |
其中正确的命题有
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:(1)函数y=
和y=x
是同一个函数,可从定义域与对应法则两个方面判断;
(2)f(x)=
(x∈[2,6])的值域为(
,2),根据函数的单调性求出值域与题设中相对照;
(3)既奇又偶的函数只有f(x)=0,由于定义域不同时,对应法则相同两函数也不是同一函数,故可举例定义域相同对应法则不同的函数例证;
(4)集合{x∈
=
,a∈N*}中只有四个元素的判断,可列举出集合中的元素进行判断;
| -2x3 |
| -2x |
(2)f(x)=
| 2 |
| x-1 |
| 2 |
| 5 |
(3)既奇又偶的函数只有f(x)=0,由于定义域不同时,对应法则相同两函数也不是同一函数,故可举例定义域相同对应法则不同的函数例证;
(4)集合{x∈
| N |
| x |
| 6 |
| a |
解答:
解:1)函数y=
和y=x
的定义域都是(-∞,0),但y=
=y=-x
与函数y=x
的解析式不一样,即对应法则不同,故不是同一个函数,故不是真命题;
(2)f(x)=
(x∈[2,6])是一个减函数,其值域为[
,2],不是(
,2),故不是真命题;
(3)既奇又偶的函数只有f(x)=0不对,因为f(x)=0(∈[-2,2])是一个即奇又偶的函数,故不是真命题;
(4)集合{x∈N|x=
,a∈N*}中只有四个元素1,2,3,6,故是真命题;
综上,正确的命题仅有④,
故答案为④.
| -2x3 |
| -2x |
| -2x3 |
| -2x |
| -2x |
(2)f(x)=
| 2 |
| x-1 |
| 2 |
| 5 |
| 2 |
| 5 |
(3)既奇又偶的函数只有f(x)=0不对,因为f(x)=0(∈[-2,2])是一个即奇又偶的函数,故不是真命题;
(4)集合{x∈N|x=
| 6 |
| a |
综上,正确的命题仅有④,
故答案为④.
点评:本题考查命题真假的判断,此类题涉及到的知识点较多,知识跨度大,需要有着比较扎实的知识与技能功底才能正确判断.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
若函数f(x)=(m-1)x2+2mx+3是偶函数,则f(x)在区间(-5,-3)上( )
| A、单调递增 | B、单调递减 |
| C、先增后减 | D、先减后增 |
已知集合A={x||x|<1},B={x|log
x>0},则A∩B=( )
| 1 |
| 3 |
| A、(0,1) | B、(-1,1) |
| C、(1,+∞) | D、∅ |
已知f(x)=2cos
x,则f(0)+f(1)+f(2)+…+f(2008)=( )
| π |
| 6 |
| A、1 | ||
B、3+
| ||
C、2+
| ||
| D、0 |
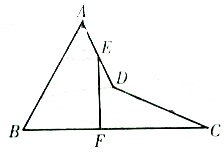 如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点,
如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点,