题目内容
若a=20.5,b=log23,c=log2
,则有( )
| ||
| 2 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |
考点:对数值大小的比较
专题:计算题,函数的性质及应用
分析:化简a=20.5=
,c=log2
=-
,判断log23>log22
=
,从而得出b>a>c.
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
解答:
解:a=20.5=
,c=log2
=-
,
log23>log22=1,
且log23>log22
=
,
故b>a>c,
故选B.
| 2 |
| ||
| 2 |
| 1 |
| 2 |
log23>log22=1,
且log23>log22
| 2 |
| 3 |
| 2 |
故b>a>c,
故选B.
点评:本题考查了对数、指数的运算及对数值的取值范围,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
设O是坐标原点,点M(x,y)是平面区域
上的动点,点N(-1,1),则
•
的取值范围是( )
|
| OM |
| ON |
| A、[-1,0] |
| B、[-1,2] |
| C、[0,1] |
| D、[0,2] |
已知m,n,l为不同的直线,α,β为不同的平面,则下列四个命题正确的是( )
| A、m,n为异面直线,m∥α,n∥α,且l⊥m,l⊥n,则l⊥α |
| B、若m∥α,且n⊥m,则有n⊥α |
| C、若α⊥β,m∥n,n⊥β,则m∥α |
| D、m与α相交但不垂直,则与直线m平行的平面不可能与平面α垂直 |
复数z=log2(m2-3m-3)+ilog2(3-m)(m∈R),如果a是纯虚数,则m的值为( )
| A、-1或4 | B、-1 | C、4 | D、3 |
若奇函数f(x)在[-6,-2]上是减函数,且最小值是1,则它在[2,6]上是( )
| A、增函数且最小值是-1 |
| B、增函数且最大值是-1 |
| C、减函数且最大值是-1 |
| D、减函数且最小值是-1 |
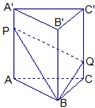 如图直三棱柱ABC-A1B1C1的体积为120,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为
如图直三棱柱ABC-A1B1C1的体积为120,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为