题目内容

复数z=log2（m2-3m-3）+ilog2（3-m）（m∈R），如果a是纯虚数，则m的值为（　　）
A、-1或4B、-1C、4D、3
考点：复数的基本概念
专题：数系的扩充和复数
分析：直接由给出的复数的实部等于0且虚部不等于0求解对数方程得答案．
解答： 解：∵z=log2（m2-3m-3）+ilog2（3-m）（m∈R）是纯虚数，
则
log2(m2-3m-3)=0
log2(3-m)≠0
，即
m2-3m-3=1
3-m≠1
，解得：m=-1．
故选：B．
点评：本题考查了复数的基本概念，考查了对数方程的解法，是基础题．
练习册系列答案
相关题目
若数列{An}满足An+1=A
 
2
n
，则称{An}是“平方递推数列”，数列{xn}、{yn}满足x1=3，以（xn，xn+1）为坐标的点在函数f（x）=3x2+2x的图象上，以（xn，yn）为坐标的点在直线y=3x+1上．
（Ⅰ）求证：数列{yn}是“平方递推数列”；
（Ⅱ）设数列{yn}的前n项之积为Tn，令zn=log ynTn，求数列{zn}的前n项和Sn．
若函数f（x）=|x+1|+|2x+a|的最小值为3，则实数a的值为
 
．
给出下列命题；
①设[x]表示不超过x的最大整数，则[log21]+[og22]+[log23]+…+[log2127]+[log2128]=649；
②定义在R上的函数f（x），函数y=f（x-1）与y=f（1-x）的图象关于y轴对称；
③函数f（x）=
x-1
2x+1
的对称中心为（-
1
2
，-
1
2
）；
④定义：若任意x∈A，总有a-x∈A（A≠∅），就称集合A为a的“闭集”，已知A⊆{1，2，3，4，5，6} 且A为6的“闭集”，则这样的集合A共有7个．其中正确的命题序号是
 
．
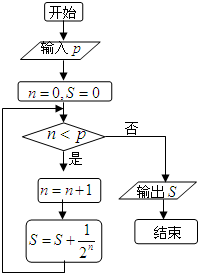
执行如图的程序框图，若输入的P是10，则输出的结果S的值为（　　）
A、1-
1
29
B、1-
1
211
C、1-
1
210
D、10-
20
210
若a=20.5，b=log23，c=log2
2
2
，则有（　　）
A、a＞b＞c
B、b＞a＞c
C、c＞a＞b
D、b＞c＞a
等差数列{an}与等比数列{bn}（n∈N*）满足：a1=b1=1，a2=b2+1，a4=b4+1．
（1）求它们的通项公式；
（2）若数列{an}的前n项和为Sn且有an＞0，数列{cn}满足cn=λ•bn+1-Sn，λ是不为0的常数．证明：λ＞2是数列{cn+1-cn}是递增数列的充要条件．
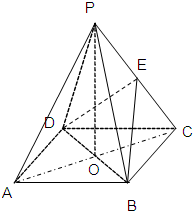如图在四棱锥P-ABCD中，底面ABCD是正方形，O是正方形的中心，
PO⊥底面ABCD，E是PC的中点．求证：
（1）PA∥平面BDE；
（2）AC⊥PB．
下图，有一个是函数f（x）=
1
3
x3+ax2+（a2-1）x+1（a∈R，a≠0）
1
3
x3+ax2+（a2-1）2+1（a∈R，a≠0）的导函数f′（x）的图象，则f（-1）等于（　　）
A、
1
3
B、-
1
3
C、
7
3
D、-
1
3
或
5
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网