题目内容
已知椭圆C:
+
=1(a>b>0)的右焦点为F(1,0),短轴的一个端点B到F的距离等于焦距.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点F的直线l和椭圆交于两点A,B,且
=2
,求直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点F的直线l和椭圆交于两点A,B,且
| AF |
| FB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由已知直接得到椭圆的半焦距和椭圆的长半轴,结合隐含条件求得b,则椭圆的方程可求;
(Ⅱ)设过点F的直线l的方程是x=my+1,和椭圆方程联立后化为关于y的一元二次方程,由
=2
得到A,B两点的纵坐标的关系,结合根与系数关系求得m的值,则直线l的方程可求.
(Ⅱ)设过点F的直线l的方程是x=my+1,和椭圆方程联立后化为关于y的一元二次方程,由
| AF |
| FB |
解答:
解:(Ⅰ)由已知得c=1,a=2c=2,
b2=a2-c2=3,
∴椭圆C的方程为
+
=1;
(Ⅱ)设直线l的方程是x=my+1,
由
,消去x并整理得(4+3m2)y2+6my-9=0.
设A(x1,y1),B(x2,y2),
则y1+y2=-
①,
y1y2=-
②,
∵
=2
,得y1=-2y2 ③,
由①②③解得m2=
,m=±
.
因此存在直线l:x=±
y+1,使得
=2
.
b2=a2-c2=3,
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设直线l的方程是x=my+1,
由
|
设A(x1,y1),B(x2,y2),
则y1+y2=-
| 6m |
| 4+3m2 |
y1y2=-
| 9 |
| 4+3m2 |
∵
| AF |
| FB |
由①②③解得m2=
| 4 |
| 5 |
2
| ||
| 5 |
因此存在直线l:x=±
2
| ||
| 5 |
| AF |
| FB |
点评:本题考查了椭圆方程的求法,考查了直线和圆锥曲线的关系,训练了向量共线的坐标表示,是压轴题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知复数z=
,其中i是虚数单位,则|z|=( )
| 2-i |
| 1-i |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若a=20.5,b=log23,c=log2
,则有( )
| ||
| 2 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |
设8(a3-1)=(a-1)(a+1)(a2+a+1),且a≠1,则a的值是( )
| A、7 | B、15 | C、35 | D、63 |
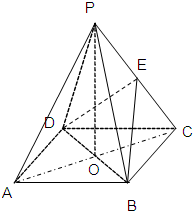 如图在四棱锥P-ABCD中,底面ABCD是正方形,O是正方形的中心,
如图在四棱锥P-ABCD中,底面ABCD是正方形,O是正方形的中心,