题目内容
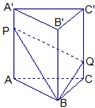 如图直三棱柱ABC-A1B1C1的体积为120,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为
如图直三棱柱ABC-A1B1C1的体积为120,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:连结A1C,设四棱锥B-APQC的高为h,由题意知S梯形APQC=S△ACC1,从而VB-APQC=
×S梯形APQC×h=
×S△ACC1×h=
VABC-A1B1C1=40.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:连结A1C,设四棱锥B-APQC的高为h,
由题意知S梯形APQC=
(AP+CQ)AC
=
(C1Q+CQ)AC
=
C1C•AC
=S△ACC1,
故VB-APQC=
×S梯形APQC×h
=
×S△ACC1×h
=VB-ACC1
=VC1-ABC
=
VABC-A1B1C1=40.
故答案为:40.
由题意知S梯形APQC=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=S△ACC1,
故VB-APQC=
| 1 |
| 3 |
=
| 1 |
| 3 |
=VB-ACC1
=VC1-ABC
=
| 1 |
| 3 |
故答案为:40.
点评:本题考查四棱锥B-APQC的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
若a=20.5,b=log23,c=log2
,则有( )
| ||
| 2 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |
设8(a3-1)=(a-1)(a+1)(a2+a+1),且a≠1,则a的值是( )
| A、7 | B、15 | C、35 | D、63 |
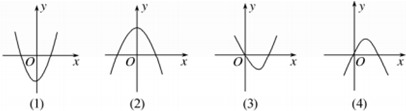
下图,有一个是函数f(x)=
x3+ax2+(a2-1)x+1(a∈R,a≠0)
x3+ax2+(a2-1)2+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)等于( )
| 1 |
| 3 |
| 1 |
| 3 |

A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
函数f(x)=|x|与g(x)=x(2-x)的单调增区间依次为( )
| A、(-∞,0],[1,+∞) |
| B、(-∞,0],(-∞,1] |
| C、[0,+∞),[1,+∞) |
| D、[0,+∞),(-∞,1] |
