题目内容
设数列|an|的前n项和为Sn,a1=7,已知an+1=6Sn+7(n=1,2,3,…)
(Ⅰ)求证:{an}是等比数列,并求an.
(Ⅱ)设bn=log7an,Tn是数列{
}的前n项和,求使Tn>
(n2-5n)对所有的n∈N+都成立的最大正整数n的值.
(Ⅰ)求证:{an}是等比数列,并求an.
(Ⅱ)设bn=log7an,Tn是数列{
| 3 |
| bnbn+1 |
| 1 |
| 4 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)在已知数列递推式中取n=n-1得另一递推式,作差后得到an+1=7an(n≥2),再求出数列第二项后即可说明{an}是等比数列,由等比数列的通项公式求得an;
(Ⅱ)把数列{an}的通项公式代入bn=log7an,进一步代入
,由裂项相消法求得数列{
}的前n项和Tn,求出其最小值,代入Tn>
(m2-5m)求解一元二次不等式得答案.
(Ⅱ)把数列{an}的通项公式代入bn=log7an,进一步代入
| 3 |
| bnbn+1 |
| 3 |
| bnbn+1 |
| 1 |
| 4 |
解答:
(Ⅰ)证明:由an+1=6Sn+7,得
an=6Sn-1+7(n≥2),
两式作差得:an+1-an=6an,即an+1=7an(n≥2).
又a1=7,代入an+1=6Sn+7,得a2=6a1+7=6×7+7=49,
∴
=7=
(n≥2),即{an}是等比数列,且首项为7,公比为7,
∴an=a1qn-1=7n;
(Ⅱ)bn=log7an=log77n=n,
=
=3(
-
),
则Tn=3(1-
+
-
+…+
-
)=3(1-
)
要使Tn>
(m2-5m)对所有的m∈N+都成立,则
(m2-5m)<(Tn)min,
而当n=1时(Tn)min=
,
∴
>
(m2-5m),即m2-5m-6<0,
∴-1<m<6.
∴使Tn>
(m2-5m)对所有的n∈N+都成立的最大正整数m的值为5.
an=6Sn-1+7(n≥2),
两式作差得:an+1-an=6an,即an+1=7an(n≥2).
又a1=7,代入an+1=6Sn+7,得a2=6a1+7=6×7+7=49,
∴
| a2 |
| a1 |
| an+1 |
| an |
∴an=a1qn-1=7n;
(Ⅱ)bn=log7an=log77n=n,
| 3 |
| bnbn+1 |
| 3 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则Tn=3(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
要使Tn>
| 1 |
| 4 |
| 1 |
| 4 |
而当n=1时(Tn)min=
| 3 |
| 2 |
∴
| 3 |
| 2 |
| 1 |
| 4 |
∴-1<m<6.
∴使Tn>
| 1 |
| 4 |
点评:本题考查了等比关系的确定,考查了裂项相消法求数列的前n项和,训练了数列不等式的解法,是中档题.

练习册系列答案
相关题目
 如图,DC垂直平面ABC,∠BAC=90°,AC=
如图,DC垂直平面ABC,∠BAC=90°,AC=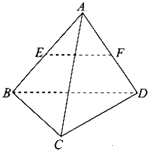 如图,四面体ABCD的每条棱长都等于2,点E,F分别为棱AB,AD的中点,则|
如图,四面体ABCD的每条棱长都等于2,点E,F分别为棱AB,AD的中点,则|