题目内容
 如图,DC垂直平面ABC,∠BAC=90°,AC=
如图,DC垂直平面ABC,∠BAC=90°,AC=| 1 |
| 2 |
(1)求证:AE⊥BC;
(2)若二面角B-AE-C的大小为120°,求k的值.
考点:二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(Ⅰ)过E点作EF⊥BC与点F,连AF,由已知条件得EF∥DC,从而EF⊥平面ABC,进而EF⊥BC,又AF⊥BC,由此能证明BC⊥AE.
(2)法一(空间向量法)以F为原点,FA为x轴,FC为y轴,FE为z轴,建立空间直角坐标系,利用向量法能求出k的值.
法二:(综合几何法)过F作FG⊥AE于G点,连GC,GB,由AE⊥BC,得AE⊥平面BCG,所以AE⊥CG,AE⊥BG,所以∠BGC为B-AE-C的平面角,由此能求出能求出k的值.
(2)法一(空间向量法)以F为原点,FA为x轴,FC为y轴,FE为z轴,建立空间直角坐标系,利用向量法能求出k的值.
法二:(综合几何法)过F作FG⊥AE于G点,连GC,GB,由AE⊥BC,得AE⊥平面BCG,所以AE⊥CG,AE⊥BG,所以∠BGC为B-AE-C的平面角,由此能求出能求出k的值.
解答:
(Ⅰ)证明:过E点作EF⊥BC与点F,
连AF,由已知条件得EF∥DC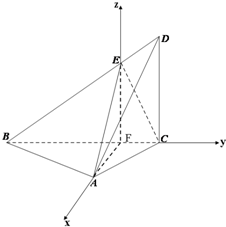
所以EF⊥平面ABC,又BC?平面ABC,所以EF⊥BC;
又∠BAC=90°,AC=
BC,所以∠ABF=30°,
所以AB=
BC,
=
=
,BF=
BC,
所以
=
=
,所以△BAF与△BCA相似,所以∠BFA=90°,即AF⊥BC,
又AF∩EF=F,于是BC⊥平面AEF,又AE?平面AEF,
所以BC⊥AE.
(2)解法一(空间向量法)
如图,以F为原点,FA为x轴,FC为y轴,FE为z轴,
建立空间直角坐标系,
则A(
,0,0),B(0,-
,0),C(0,
,0),E(0,0,
),
于是
=(-
,0,
),
=(-
,
,0),
=(-
,-
,0),
设平面ABE的法向量为
=(x1,y1,z1),
则
,令z1=1,得
=(
,-
,1).
设平面ACE的法向量为
=(x2,y2,z2),
则
,令z2=1,得
=(
,
,1),|cos120°|=
=
,解得:k=
.
解法二:(综合几何法)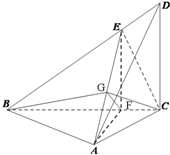
过F作FG⊥AE于G点,连GC,GB,
由AE⊥BC,得AE⊥平面BCG,所以AE⊥CG,AE⊥BG,
所以∠BGC为B-AE-C的平面角,
设AC=1,则AF=
,EF=
,所以GF=
,
于是GB=3
,GC=
,
于是由cos120°=
,得到k=
.
连AF,由已知条件得EF∥DC

所以EF⊥平面ABC,又BC?平面ABC,所以EF⊥BC;
又∠BAC=90°,AC=
| 1 |
| 2 |
所以AB=
| ||
| 2 |
| BE |
| BD |
| BF |
| BC |
| 3 |
| 4 |
| 3 |
| 4 |
所以
| BF |
| AB |
| AB |
| BC |
| ||
| 2 |
又AF∩EF=F,于是BC⊥平面AEF,又AE?平面AEF,
所以BC⊥AE.
(2)解法一(空间向量法)
如图,以F为原点,FA为x轴,FC为y轴,FE为z轴,
建立空间直角坐标系,
则A(
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4k |
于是
| AE |
| ||
| 2 |
| 3 |
| 4k |
| AC |
| ||
| 2 |
| 1 |
| 2 |
| AB |
| ||
| 2 |
| 3 |
| 2 |
设平面ABE的法向量为
| n1 |
则
|
| n1 |
| ||
| 2k |
| 1 |
| 2k |
设平面ACE的法向量为
| n2 |
则
|
| n2 |
| ||
| 2k |
| 3 |
| 2k |
|
| ||||
|
|
| 1 | ||||||||
|
|
解法二:(综合几何法)

过F作FG⊥AE于G点,连GC,GB,
由AE⊥BC,得AE⊥平面BCG,所以AE⊥CG,AE⊥BG,
所以∠BGC为B-AE-C的平面角,
设AC=1,则AF=
| ||
| 2 |
| 3 |
| 4k |
| 3 | ||
2
|
于是GB=3
|
|
于是由cos120°=
| BG2+CG2-BC2 |
| 2BG•CG |
|
点评:本题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
设x,y满足约束条件
( )
|
| A、6 | ||
B、
| ||
| C、7 | ||
D、
|
设函数f(x)=2sin(2x+
)(x∈[-
,
]),在区间D上单调递增,则区间D可以是( )
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
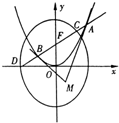 已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A、B两点.
已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A、B两点.