题目内容
已知数列{an}的前n项和为Sn,其中a1=
,2an=an-1(n≥2);等差数列{bn},其中b3=2,b5=6.
(1)求数列{an}的通项公式;
(2)在数列{bn}中是否存在一项bm(m为正整数),使得b3,b5,bm成等比数列,若存在求m的值;若不存在,请说明理由.
(3)若cn=(bn+3)an,求数列{cn}的前n项和Tn.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)在数列{bn}中是否存在一项bm(m为正整数),使得b3,b5,bm成等比数列,若存在求m的值;若不存在,请说明理由.
(3)若cn=(bn+3)an,求数列{cn}的前n项和Tn.
考点:数列的求和,等比数列的性质,数列递推式
专题:等差数列与等比数列
分析:(1)直接由已知可知数列{an}是以a1=
为首项,以2为公比的等比数列,由等比数列的通项公式得答案;
(2)由已知求出等差数列的公差,代入等差数列的通项公式求得bn,假设b3,b5,bm成等比数列,由等比数列的性质列式求得m的值;
(3)把{an}的通项公式和{bn}的通项公式代入cn=(bn+3)an,由错位相减法求得数列{cn}的前n项和Tn.
| 1 |
| 2 |
(2)由已知求出等差数列的公差,代入等差数列的通项公式求得bn,假设b3,b5,bm成等比数列,由等比数列的性质列式求得m的值;
(3)把{an}的通项公式和{bn}的通项公式代入cn=(bn+3)an,由错位相减法求得数列{cn}的前n项和Tn.
解答:
解:(1)由已知可得,数列{an}是以a1=
为首项,以2为公比的等比数列,
∴an=a1qn-1=
•2n-1=2n-2;
(2)在等差数列{bn}中,由b3=2,b5=6,得d=
=
=2,
∴bn=b2+(n-2)d=2+2(n-2)=2n-2,
若存在一项bm,使得b3,b5,bm成等比数列,则b52=b3•bm,
即82=4(2m-2),解得m=9;
(3)由cn=(bn+3)an,得cn=(2n+1)2n-2,
∴数列{cn}的前n项和:
Tn=3•2-1+5•20+…+(2n-1)•2n-3+(2n+1)•2n-2,
2Tn=3•20+5•21+…+(2n-1)•2n-2+(2n+1)•2n-1.
∴-Tn=
+21+22+…+2n-1-(2n+1)•2n-1=
+
-(2n+1)•2n-1
=
+2n-2-(2n+1)•2n-1.
∴Tn=(n-
)•2n+
.
| 1 |
| 2 |
∴an=a1qn-1=
| 1 |
| 2 |
(2)在等差数列{bn}中,由b3=2,b5=6,得d=
| b5-b3 |
| 5-3 |
| 6-2 |
| 2 |
∴bn=b2+(n-2)d=2+2(n-2)=2n-2,
若存在一项bm,使得b3,b5,bm成等比数列,则b52=b3•bm,
即82=4(2m-2),解得m=9;
(3)由cn=(bn+3)an,得cn=(2n+1)2n-2,
∴数列{cn}的前n项和:
Tn=3•2-1+5•20+…+(2n-1)•2n-3+(2n+1)•2n-2,
2Tn=3•20+5•21+…+(2n-1)•2n-2+(2n+1)•2n-1.
∴-Tn=
| 3 |
| 2 |
| 3 |
| 2 |
| 2(1-2n-1) |
| 1-2 |
=
| 3 |
| 2 |
∴Tn=(n-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了等比关系的确定,考查了等差数列和等比数列的通项公式,考查了错位相减法求数列的和,是中档题.

练习册系列答案
相关题目
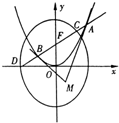 已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A、B两点.
已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A、B两点.