题目内容
已知x2-y2=1,求
+
范围.
| 1 |
| x2 |
| 2y |
| x |
考点:双曲线的参数方程,简单线性规划的应用
专题:坐标系和参数方程
分析:本题可以先利用用参数方程表示双曲线,再利用参数方程化简所示代数式,利用配方法、结合函数图象,研究二次函数的最值,得到本题结论.
解答:
解:∵x2-y2=1,
∴
,(θ为参数,θ≠kπ+
,k∈Z),
∴
+
=cos2θ+
=cos2θ+sinθ
=-sin2θ+sinθ+1
=-(sinθ-
)2+
.
∵θ≠kπ+
,k∈Z,
∴sinθ∈(-1,1),
∵当sinθ=-1时,-(sinθ-
)2+
=-
+
=-1,
当sinθ=
时,-(sinθ-
)2+
=
,
∴-1<
+
≤
.
∴
+
的取值范围是:(-1,
].
∴
|
| π |
| 2 |
∴
| 1 |
| x2 |
| 2y |
| x |
| 2tanθ |
| secθ |
=cos2θ+sinθ
=-sin2θ+sinθ+1
=-(sinθ-
| 1 |
| 2 |
| 5 |
| 4 |
∵θ≠kπ+
| π |
| 2 |
∴sinθ∈(-1,1),
∵当sinθ=-1时,-(sinθ-
| 1 |
| 2 |
| 5 |
| 4 |
| 9 |
| 4 |
| 5 |
| 4 |
当sinθ=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
∴-1<
| 1 |
| x2 |
| 2y |
| x |
| 5 |
| 4 |
∴
| 1 |
| x2 |
| 2y |
| x |
| 5 |
| 4 |
点评:本题考查了双曲线的参数方程及其应用,本题难度不大,属于基础题.

练习册系列答案
相关题目
若以椭圆
+
=1(a>b>0)的右焦点F为圆心,a为半径的圆与椭圆的右准线交于不同两点,则该椭圆的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||||
B、(
| ||||
C、(0,
| ||||
D、(
|
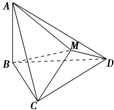 如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2
如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2