题目内容
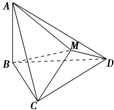 如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2
如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2| 3 |
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:首先利用已知条件,过点M作CD的垂线交CD于E点,过E作EF⊥BC于F.连接BE,根据△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,利用勾股定理分别求得:ME=
,AC=4,BE=
,EF=
,BM=
,进一步设点A到平面MBC的距离为h,利用VA-BCM=VM-ABC根据:
•S△BCM•h=
•S△ABC•EF,解得h的值.
| 3 |
| 3 |
| ||
| 2 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:过点M作CD的垂线交CD于E点,过E作EF⊥BC于F.连接BE,
根据△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,利用勾股定理
解得:ME=
,AC=4,BE=
,EF=
,BM=
设点A到平面MBC的距离为h
利用VA-BCM=VM-ABC
则:
•S△BCM•h=
•S△ABC•EF,
解得:h=
.
故答案为:
.
根据△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,利用勾股定理
解得:ME=
| 3 |
| 3 |
| ||
| 2 |
| 6 |
设点A到平面MBC的距离为h
利用VA-BCM=VM-ABC
则:
| 1 |
| 3 |
| 1 |
| 3 |
解得:h=
2
| ||
| 5 |
故答案为:
2
| ||
| 5 |
点评:本题考查的知识要点:面面垂直与线面垂直间的转化,勾股定理的应用,锥体的体积的应用,属于基础题型.

练习册系列答案
相关题目
集合A={x||x-1|<2},B={x|2-x-x2>0},则A∩B=( )
| A、(-2,3) |
| B、(-1,1) |
| C、(1,3) |
| D、(-1,2) |
已知不同的三点A、B、C满足
=λ
(λ∈R,λ≠0),使得关于x的方程x2
+x
-
=
有解(点O不在直线AB上),则此方程在实数范围内的解集为( )
| AB |
| BC |
| OA |
| OB |
| OC |
| 0 |
| A、∅ | ||||||||
| B、{-1,0} | ||||||||
| C、{-1} | ||||||||
D、{
|
 如图,在直角坐标系中,点O为原点,点A的坐标为(4,3),⊙A的半径为2,过点A作平行于x轴的直线l,点P在l上运动.
如图,在直角坐标系中,点O为原点,点A的坐标为(4,3),⊙A的半径为2,过点A作平行于x轴的直线l,点P在l上运动.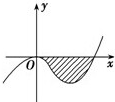 已知函数f(x)=x3+ax2+bx+c(a、b、c∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成的区域(图中阴影部分)的面积为
已知函数f(x)=x3+ax2+bx+c(a、b、c∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成的区域(图中阴影部分)的面积为