题目内容
已知集合A={a|
+kπ<α<
+kπ,k∈Z},集合B={β|-
+2kπ<β<
+2kπ,k∈Z},求A∩B.
| π |
| 6 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
考点:交集及其运算
专题:集合
分析:利用交集的性质和角的周期性求解.
解答:
解:∵集合A={a|
+kπ<α<
+kπ,k∈Z},
集合B={β|-
+2kπ<β<
+2kπ,k∈Z},
∴A∩B={α|
+2kπ,
+2kπ,k∈Z}.
| π |
| 6 |
| π |
| 2 |
集合B={β|-
| π |
| 4 |
| π |
| 4 |
∴A∩B={α|
| π |
| 6 |
| π |
| 4 |
点评:本题考查两个集合的交集的求法,是基础题,解题时要认真审题,注意交集的性质的合理运用.

练习册系列答案
相关题目
已知不同的三点A、B、C满足
=λ
(λ∈R,λ≠0),使得关于x的方程x2
+x
-
=
有解(点O不在直线AB上),则此方程在实数范围内的解集为( )
| AB |
| BC |
| OA |
| OB |
| OC |
| 0 |
| A、∅ | ||||||||
| B、{-1,0} | ||||||||
| C、{-1} | ||||||||
D、{
|
已知A、B、C、D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=4,AB=2
,则该球的表面积为( )
| 3 |
| A、8π | B、16π |
| C、32π | D、64π |
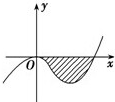 已知函数f(x)=x3+ax2+bx+c(a、b、c∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成的区域(图中阴影部分)的面积为
已知函数f(x)=x3+ax2+bx+c(a、b、c∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成的区域(图中阴影部分)的面积为