题目内容
设A={4，a}，B={2，ab}，若A=B，则a+b= ．
考点：集合的相等
专题：集合
分析：利用集合相等，集合元素相同解答．
解答：
解：因为A={4，a}，B={2，ab}，A=B，
所以
，解得a=2，b=2，
所以a+b=4；
故答案为：4
所以
|
所以a+b=4；
故答案为：4
点评：本题考查了集合的相等，如果两个集合相等，那么两个集合元素完全相同．
练习册系列答案
相关题目
复数
+
=（ ）
| 1 |
| 1-i |
| i |
| 1+i |
| A、-i |
| B、1-i |
| C、1+i D．i |
设a=2
，b=log2
，c=log
，则（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、c＞b＞a |
| B、c＞a＞b |
| C、a＞b＞c |
| D、a＞b＞c |
已知命题p：?x∈R，tanx＜1，则（ ）
| A、￢p：?x∈R，tanx＞1 |
| B、￢p：?x∈R，tanx≥1 |
| C、￢p：?x∈R，tanx＞1 |
| D、￢p：?x∈R，tanx≥1 |
集合A={x||x-1|＜2}，B={x|2-x-x2＞0}，则A∩B=（ ）
| A、（-2，3） |
| B、（-1，1） |
| C、（1，3） |
| D、（-1，2） |
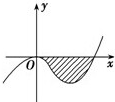已知函数f（x）=x3+ax2+bx+c（a、b、c∈R）的图象如图所示，它与x轴在原点处相切，且x轴与函数图象所围成的区域（图中阴影部分）的面积为