题目内容
对于任意的实数a(a≠0)和b,不等式|a+b|+|a-b|≥M•|a|恒成立,记实数M的最大值是m.
(Ⅰ)求m的值;
(Ⅱ)解不等式|x-1|+|x-2|≤m.
(Ⅰ)求m的值;
(Ⅱ)解不等式|x-1|+|x-2|≤m.
考点:绝对值不等式的解法,绝对值三角不等式
专题:计算题,不等式的解法及应用
分析:(Ⅰ)由题意可得M≤
,对于任意的实数a(a≠0)和b恒成立,再由
≥2可得,M≤2,由此可得m的值;
(Ⅱ)由于|x-1|+|x-2|表示数轴上的x对应点到1和2对应点的距离之和,而数轴上
和
对应点到1和2对应点的距离之和正好等于2,由此求得|x-1|+|x-2|≤2的解集.
| |a+b|+|a-b| |
| |a| |
| |a+b|+|a-b| |
| |a| |
(Ⅱ)由于|x-1|+|x-2|表示数轴上的x对应点到1和2对应点的距离之和,而数轴上
| 1 |
| 2 |
| 5 |
| 2 |
解答:
解:(Ⅰ)不等式|a+b|+|a-b|≥M•|a|恒成立,
即M≤
对于任意的实数a(a≠0)和b恒成立,
故只要左边恒小于或等于右边的最小值.
因为|a+b|+|a-b|≥|(a+b)+(a-b)|=2|a|,
当且仅当(a-b)(a+b)≥0时等号成立,
即|a|≥|b|时,
≥2成立,
也就是
的最小值是2,
故M的最大值为2,即 m=2.
(Ⅱ)不等式|x-1|+|x-2|≤m即|x-1|+|x-2|≤2.
由于|x-1|+|x-2|表示数轴上的x对应点到1和2对应点的距离之和,
而数轴上
和
对应点到1和2对应点的距离之和正好等于2,
故|x-1|+|x-2|≤2的解集为:{x|
≤x≤
}.
即M≤
| |a+b|+|a-b| |
| |a| |
故只要左边恒小于或等于右边的最小值.
因为|a+b|+|a-b|≥|(a+b)+(a-b)|=2|a|,
当且仅当(a-b)(a+b)≥0时等号成立,
即|a|≥|b|时,
| |a+b|+|a-b| |
| |a| |
也就是
| |a+b|+|a-b| |
| |a| |
故M的最大值为2,即 m=2.
(Ⅱ)不等式|x-1|+|x-2|≤m即|x-1|+|x-2|≤2.
由于|x-1|+|x-2|表示数轴上的x对应点到1和2对应点的距离之和,
而数轴上
| 1 |
| 2 |
| 5 |
| 2 |
故|x-1|+|x-2|≤2的解集为:{x|
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查绝对值的意义,绝对值不等式的解法,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
设函数f(x)=x2+2ax+b2,若a∈[0,2],b∈[0,3],则函数f(x)有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
方程log2x+x-2=0的解所在的区间为( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
若直线ax+(1-a)y=3与(a-1)x+(2a+3)y=2互相垂直,则a等于( )
| A、3 | ||
| B、1 | ||
C、0或-
| ||
| D、1或-3 |
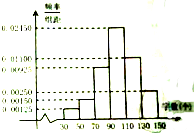 重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.
重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.