题目内容
已知向量
=3
-2
，
=4
-
，其中
=（1，0），
=（0，1）．
（1）求：
，
；
（2）求：|
+
|及
与
的夹角的余弦值．
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
（1）求：
| a |
| b |
（2）求：|
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：（1）运用向量的和差运算公式，即可得到；
（2）求出向量的数量积和两向量的和的平方，即可得到：|
+
|，再由向量的夹角公式cos＜
，
＞=
即可得到答案．
（2）求出向量的数量积和两向量的和的平方，即可得到：|
| a |
| b |
| a |
| b |
| ||||
|
|
解答：
解：（1）
=3（1，0）-2（0，1）=（3，-2），
=4（1，0）-（0，1）=（4，-1），
（2）
•
=3×4+（-2）×（-1）=14．
∴|
+
|2=（
+
）2=
2+2
•
+
2=|
|2+28+|
|2=13+28+17=58，
∴|a+b|=
．
∴cos＜
，
＞=
=
=
．
| a |
| b |
（2）
| a |
| b |
∴|
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
∴|a+b|=
| 58 |
∴cos＜
| a |
| b |
| ||||
|
|
| 14 | ||||
|
14
| ||
| 221 |
点评：本题主要考查向量的和、差以及数量积的坐标运算，向量的模的运算，向量的夹角的余弦，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知一个正四面体的俯视图如图所示，其中四边形ABCD是边长为3| 2 |
| A、6π | B、54π |
| C、12π | D、48π |
已知点F1，F2分别是双曲线C：
-
=1（a＞0，b＞0）的左、右焦点，过F2且垂直于x轴的直线与C交于A，B两点，若△ABF1为等腰直角三角形，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
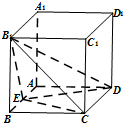如图，正方体ABCD-A1B1C1D1中，E是AB的中点
根据如图所示算法语句，将输出的A值依次分别记为a1，a2，…，an，…，a2014