题目内容
已知圆心为C(-2,6)的圆经过点M(0,6-2
).
(Ⅰ)求圆C的标准方程;
(Ⅱ)若直线l过点P(0,5)且被圆C截得的线段长为4
,求直线l的方程;
(Ⅲ)是否存在斜率是1的直线l′,使得以l′被圆C所截得的弦EF为直径的圆经过原点?若存在,试求出直线l′的方程;若不存在,请说明理由.
| 3 |
(Ⅰ)求圆C的标准方程;
(Ⅱ)若直线l过点P(0,5)且被圆C截得的线段长为4
| 3 |
(Ⅲ)是否存在斜率是1的直线l′,使得以l′被圆C所截得的弦EF为直径的圆经过原点?若存在,试求出直线l′的方程;若不存在,请说明理由.
考点:圆的标准方程,直线与圆的位置关系
专题:直线与圆
分析:(Ⅰ)先求出圆C的半径为|CM|的值,可得圆C的标准方程.
(Ⅱ)如图所示,设直线l与圆C交于A、B 两点,且D是AB的中点,在直角三角形ACD中,可得CD=2,即点C到直线l的距离为2.再分当所求直线l的斜率存在和直线l的斜率不存在两种情况,分别求得直线的方程.
(Ⅲ)假设存在直线l′满足题设条件,设l′的方程为y=x+m,可得 N(
,
),CN=
.
再由 CE2=CN2+EN2,化简得 m2-8m+20=0,根据方程m2-8m+20=0没有实数解,可得不存在满足题设条件的直线l′.
(Ⅱ)如图所示,设直线l与圆C交于A、B 两点,且D是AB的中点,在直角三角形ACD中,可得CD=2,即点C到直线l的距离为2.再分当所求直线l的斜率存在和直线l的斜率不存在两种情况,分别求得直线的方程.
(Ⅲ)假设存在直线l′满足题设条件,设l′的方程为y=x+m,可得 N(
| 4-m |
| 2 |
| m+4 |
| 2 |
| |m-8| | ||
|
再由 CE2=CN2+EN2,化简得 m2-8m+20=0,根据方程m2-8m+20=0没有实数解,可得不存在满足题设条件的直线l′.
解答:
 解:(Ⅰ)圆C的半径为|CM|=4,∴圆C的标准方程为 (x+2)2+(y-6)2=16.
解:(Ⅰ)圆C的半径为|CM|=4,∴圆C的标准方程为 (x+2)2+(y-6)2=16.
(Ⅱ)如图所示,设直线l与圆C交于A、B 两点,且D是AB的中点,
则AB=4
,AD=2
且 CD⊥AB,
∵圆C的半径为4,即AC=4,
∴在直角三角形ACD中,可得 CD=
=2,即点C到直线l的距离为2.
(i)当所求直线l的斜率存在时,设所求直线的方程为y=kx+5,即kx-y+5=0,
由点到直线的距离公式得:
=2,解得 k=
.
∴此时直线l的方程为3x-4y+20=0.
(ii)当直线l的斜率不存在时,直线l的方程为x=0.
将x=0代入圆C的方程化简可得(y-6)2=12,y=6±2
,∴弦长为4
,满足条件.
∴所求直线的方程为 3x-4y+20=0,或 x=0.
(Ⅲ)假设存在直线l′满足题设条件,设l′的方程为y=x+m,
则EF的中点N是两直线 y=x+m与y+6=-(x+2)的交点,即 N(
,
),
∴CN=
=
.
∵以EF为直径的圆经过原点,∴OE⊥OF,∴EN=ON=
.
又∵CN⊥EF,CE2=CN2+EN2,
∴(
)2+(
)2+(
)2=16,化简得 m2-8m+20=0,
∵方程m2-8m+20=0没有实数解,
∴不存在满足题设条件的直线l′.
 解:(Ⅰ)圆C的半径为|CM|=4,∴圆C的标准方程为 (x+2)2+(y-6)2=16.
解:(Ⅰ)圆C的半径为|CM|=4,∴圆C的标准方程为 (x+2)2+(y-6)2=16.(Ⅱ)如图所示,设直线l与圆C交于A、B 两点,且D是AB的中点,
则AB=4
| 3 |
| 3 |
∵圆C的半径为4,即AC=4,
∴在直角三角形ACD中,可得 CD=
| AC2-AD2 |
(i)当所求直线l的斜率存在时,设所求直线的方程为y=kx+5,即kx-y+5=0,
由点到直线的距离公式得:
| |-2k-6+5| | ||
|
| 3 |
| 4 |
∴此时直线l的方程为3x-4y+20=0.
(ii)当直线l的斜率不存在时,直线l的方程为x=0.
将x=0代入圆C的方程化简可得(y-6)2=12,y=6±2
| 3 |
| 3 |
∴所求直线的方程为 3x-4y+20=0,或 x=0.
(Ⅲ)假设存在直线l′满足题设条件,设l′的方程为y=x+m,
则EF的中点N是两直线 y=x+m与y+6=-(x+2)的交点,即 N(
| 4-m |
| 2 |
| m+4 |
| 2 |
∴CN=
(
|
| |m-8| | ||
|
∵以EF为直径的圆经过原点,∴OE⊥OF,∴EN=ON=
(
|
又∵CN⊥EF,CE2=CN2+EN2,
∴(
| 4-m |
| 2 |
| m+4 |
| 2 |
| |m-8| | ||
|
∵方程m2-8m+20=0没有实数解,
∴不存在满足题设条件的直线l′.
点评:本题主要考查求圆的标准方程的方法,直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 若函数f(x)=Asin(2x+φ)(A>0,-
若函数f(x)=Asin(2x+φ)(A>0,-| π |
| 2 |
| π |
| 2 |
| A、-2 | ||
| B、-1 | ||
C、-
| ||
D、-
|
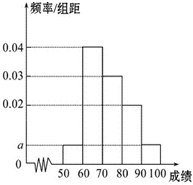 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]