题目内容
 根据如图所示算法语句,将输出的A值依次分别记为a1,a2,…,an,…,a2014
根据如图所示算法语句,将输出的A值依次分别记为a1,a2,…,an,…,a2014(1)求数列{an}的通项公式;
(2)令bn=
| 22n-1 |
| an•an+1 |
| 1 |
| 3 |
考点:数列的求和,程序框图
专题:等差数列与等比数列
分析:(1)依题意,an=(an-an-1)+…+(a2-a1)+a1=3(22n-3+22n-5+…+2)+1=22n-1-1,利用等比数列的求和公式可得an=22n-1-1,再验证a1=1,满足上式即可;
(2)由(1)知an=22n-1-1,利用裂项法易知bn=
=
(
-
),从而可知结论成立.
(2)由(1)知an=22n-1-1,利用裂项法易知bn=
| 22n-1 |
| an•an+1 |
| 1 |
| 3 |
| 1 |
| 22n-1-1 |
| 1 |
| 22n+1-1 |
解答:
(1)解:由已知,当n≥2时,an=(an-an-1)+…+(a2-a1)+a1
=3(22n-3+22n-5+…+2)+1=22n-1-1,
而a1=1,满足上式,
所以数列{an}的通项公式为:an=22n-1-1;
(2)证明:由(1)知an=22n-1-1,
所以bn=
=
=
(
-
),
∴Sn=
[(
-
)+(
-
)+…+(
-
)]
=
(
-
)<
<
.
故对于任意的n∈N*,Sn<
(n∈N*,n≤2014).
=3(22n-3+22n-5+…+2)+1=22n-1-1,
而a1=1,满足上式,
所以数列{an}的通项公式为:an=22n-1-1;
(2)证明:由(1)知an=22n-1-1,
所以bn=
| 22n-1 |
| an•an+1 |
| 22n-1 |
| (22n-1-1)(22n+1-1) |
| 1 |
| 3 |
| 1 |
| 22n-1-1 |
| 1 |
| 22n+1-1 |
∴Sn=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 31 |
| 1 |
| 22n-1-1 |
| 1 |
| 22n+1-1 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 22n+1-1 |
| 1 |
| 6 |
| 1 |
| 3 |
故对于任意的n∈N*,Sn<
| 1 |
| 3 |
点评:本题考查数列的求和,着重考查递推关系的应用,考查列项相消法求和,考查程序框图的理解与应用,属于中档题.

练习册系列答案
相关题目
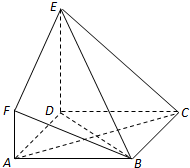 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.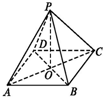 如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,运用三段论证明BD⊥平面PAC.
如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,运用三段论证明BD⊥平面PAC.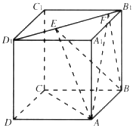 如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=