题目内容
设Sn为数列{an}的前n项和（n=1，2，3，…），按如下方式定义数列{an}：a1=m（m∈N*），对任意k∈N*，k＞1，设ak为满足0≤ak≤k-1的整数，且k整除Sk．
（1）当m=9时，试给出{an}的前6项；
（2）证明：?k∈N*，有
＜
+1；
（3）证明：对任意的m，数列{an}必从某项起成为常数列．
（1）当m=9时，试给出{an}的前6项；
（2）证明：?k∈N*，有
| Sk+1 |
| k+1 |
| Sk |
| k |
（3）证明：对任意的m，数列{an}必从某项起成为常数列．
考点：数列的应用
专题：综合题,等差数列与等比数列
分析：（1）利用定义，可写出{an}的前6项；
（2）利用放缩法证明k∈N*，有
＜
+1；
（3）确定数列{
}必将从某项起变为常数，再证明：对任意的m，数列{an}必从某项起成为常数列．
（2）利用放缩法证明k∈N*，有
| Sk+1 |
| k+1 |
| Sk |
| k |
（3）确定数列{
| Sk |
| k |
解答：
（1）解：m=9时，数列为9，1，2，0，3，3，3，3，
即前六项为9，1，2，0，3，3．
（2）证明：?k∈N*，有
＜
=
≤
=
+1；
（3）证明：∵?k∈N*，有
∈N*，
由（2）可得
＜
，
∵
=m为定值且
单调不增，
∴数列{
}必将从某项起变为常数，
不妨设从l项起
为常数，则
=
，
于是al+1=Sl+1-Sl=
，
∴al+2=al+1=
，
∴数列{an}当n≥l+1时成为常数列．
即前六项为9，1，2，0，3，3．
（2）证明：?k∈N*，有
| Sk+1 |
| k+1 |
| Sk+1 |
| k |
| Sk+ak+1 |
| k |
| Sk+k |
| k |
| Sk |
| k |
（3）证明：∵?k∈N*，有
| Sk |
| k |
由（2）可得
| Sk+1 |
| k+1 |
| Sk |
| k |
∵
| S1 |
| 1 |
| Sk |
| k |
∴数列{
| Sk |
| k |
不妨设从l项起
| Sk |
| k |
| Sl+1 |
| l+1 |
| Sl |
| l |
于是al+1=Sl+1-Sl=
| Sl |
| l |
∴al+2=al+1=
| Sl |
| l |
∴数列{an}当n≥l+1时成为常数列．
点评：本题考查数列的应用，考查新定义，考查学生分析解决问题的能力，正确理解新定义是关键．
练习册系列答案
名校课堂系列答案
相关题目
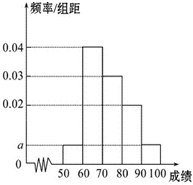某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]
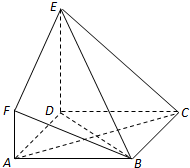如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE与平面ABCD所成角为60°．
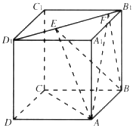如图，正方体ABCD-A1B1C1D1的棱线长为1，线段B1D1上有两个动点E，F，且EF=