题目内容
已知函数f(x)=ax2-x+lnx(a>0).
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线斜率为2,求a的值及在该点处的切线方程;
(Ⅱ)若f(x)是单调函数,求a的取值范围.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线斜率为2,求a的值及在该点处的切线方程;
(Ⅱ)若f(x)是单调函数,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,根据导数的几何意义即可求a的值及在该点处的切线方程;
(Ⅱ)根据函数是单调函数,则导数的符号相同,建立条件关系即可得到结论.
(Ⅱ)根据函数是单调函数,则导数的符号相同,建立条件关系即可得到结论.
解答:
解:(Ⅰ)f′(x)=2ax-1+
.…(2分)
由题设,f′(1)=2a=2,a=1,
此时f(1)=0,切线方程为y=2(x-1),
即2x-y-2=0.…(5分)
(Ⅱ)f′(x)=
.
当a≥
时,△=1-8a≤0,f′(x)≥0,
f(x)在(0,+∞)单调递增.…(9分)
当0<a<
时,△>0,方程2ax2-x+1=0有两个不相等的正根
x1=
,x2=
.
当x∈(0,x1)∪(x2,+∞)时,f(x)>0,当x∈(x1,x2)时,f(x)<0,
这时f (x)不是单调函数.
综上,a的取值范围是[
,+∞).…(12分)
| 1 |
| x |
由题设,f′(1)=2a=2,a=1,
此时f(1)=0,切线方程为y=2(x-1),
即2x-y-2=0.…(5分)
(Ⅱ)f′(x)=
| 2ax2-x+1 |
| x |
当a≥
| 1 |
| 8 |
f(x)在(0,+∞)单调递增.…(9分)
当0<a<
| 1 |
| 8 |
x1=
1-
| ||
| 4a |
1+
| ||
| 4a |
当x∈(0,x1)∪(x2,+∞)时,f(x)>0,当x∈(x1,x2)时,f(x)<0,
这时f (x)不是单调函数.
综上,a的取值范围是[
| 1 |
| 8 |
点评:本题主要考查主要考查导数的应用,要求熟练掌握导数的几何意义,以及函数单调性和导数之间的关系.

练习册系列答案
相关题目
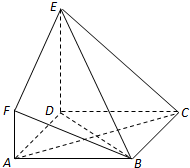 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.