题目内容
6.直线$x+\sqrt{3}y-1=0$的倾斜角为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 由直线的方程可得斜率等于-$\frac{\sqrt{3}}{3}$,设直线的倾斜角为θ,则tanθ=-$\frac{\sqrt{3}}{3}$,0≤θ<π,由此解得 θ的值.
解答 解:∵直线$x+\sqrt{3}y-1=0$的斜率等于-$\frac{\sqrt{3}}{3}$,设直线$x+\sqrt{3}y-1=0$的倾斜角为θ,
则tanθ=-$\frac{\sqrt{3}}{3}$,0≤θ<π,解得 θ=$\frac{5π}{6}$,
故选D.
点评 本题主要考查直线的倾斜角和斜率的关系,以及倾斜角的取值范围,已知三角函数值求角的大小,属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
16.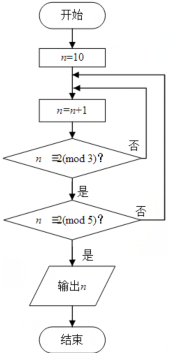 若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
 若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
17.三位男同学两位女同学站成一排,女同学不站两端的排法总数为( )
| A. | 6 | B. | 36 | C. | 48 | D. | 120 |
14. 我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )
我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )
 我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )
我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )| A. | 44,45,56 | B. | 44,43,57 | C. | 44,43,56 | D. | 45,43,57 |
11.某班50人的一次竞赛成绩的频数分布如下:[60,70):3人,[70,80):16人,[80,90):24人,[90,100]:7人,利用各组区间中点值,可估计本次比赛该班的平均分为( )
| A. | 56 | B. | 68 | C. | 78 | D. | 82 |
15.设集合M=[0,$\frac{1}{2}$),N=[$\frac{1}{2}$,1],函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{2},x∈M}\\{2(1-x),x∈N}\end{array}\right.$.若x0∈M且f(f(x0))∈M,则x0的取值范围为( )
| A. | (0,$\frac{1}{4}$] | B. | [0,$\frac{3}{8}$] | C. | ($\frac{1}{4}$,$\frac{1}{2}$] | D. | ($\frac{1}{4}$,$\frac{1}{2}$) |
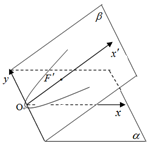 具有公共y轴的两个直角坐标平面α和β所成的二面角α-y轴-β等于60°,已知β内的曲线C'的方程是y2=4x',曲线C'在α内的射影在平面α内的曲线方程为y2=2px,则p=1.
具有公共y轴的两个直角坐标平面α和β所成的二面角α-y轴-β等于60°,已知β内的曲线C'的方程是y2=4x',曲线C'在α内的射影在平面α内的曲线方程为y2=2px,则p=1. 如图,在三棱锥S-ABC中,△ABC为直角三角形,且∠ACB=90°,SA⊥平面ABC,AD⊥SC.
如图,在三棱锥S-ABC中,△ABC为直角三角形,且∠ACB=90°,SA⊥平面ABC,AD⊥SC.