题目内容
15.设集合M=[0,$\frac{1}{2}$),N=[$\frac{1}{2}$,1],函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{2},x∈M}\\{2(1-x),x∈N}\end{array}\right.$.若x0∈M且f(f(x0))∈M,则x0的取值范围为( )| A. | (0,$\frac{1}{4}$] | B. | [0,$\frac{3}{8}$] | C. | ($\frac{1}{4}$,$\frac{1}{2}$] | D. | ($\frac{1}{4}$,$\frac{1}{2}$) |
分析 根据分段函数的解析即可求出x0的范围.
解答 解:∵0≤x0<$\frac{1}{2}$,
∴f(x0))∈[$\frac{1}{2}$,1]⊆N,
∴f(f(x0))=2(1-f(x0))=2[1-(x0+$\frac{1}{2}$)]=2($\frac{1}{2}$-x0),
∵f(f(x0))∈M,
∴0≤2($\frac{1}{2}$-x0)<$\frac{1}{2}$,
∴$\frac{1}{4}$<x0≤$\frac{1}{2}$
∵0≤x0<$\frac{1}{2}$,
∴$\frac{1}{4}$<x0<$\frac{1}{2}$
故选:D
点评 本题考查 了集合的含义及表示、函数的单调性、最值、以及分段函数的性质,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
6.直线$x+\sqrt{3}y-1=0$的倾斜角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
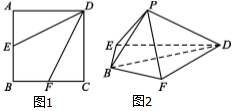 如图,在边长为2的正方形ABCD中,点E,F分别是AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.
如图,在边长为2的正方形ABCD中,点E,F分别是AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.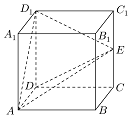 如图,已知正方形ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则三棱锥D1-ADE的体积为$\frac{4}{3}$.
如图,已知正方形ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则三棱锥D1-ADE的体积为$\frac{4}{3}$.