题目内容
1.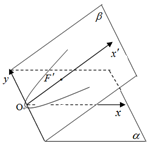 具有公共y轴的两个直角坐标平面α和β所成的二面角α-y轴-β等于60°,已知β内的曲线C'的方程是y2=4x',曲线C'在α内的射影在平面α内的曲线方程为y2=2px,则p=1.
具有公共y轴的两个直角坐标平面α和β所成的二面角α-y轴-β等于60°,已知β内的曲线C'的方程是y2=4x',曲线C'在α内的射影在平面α内的曲线方程为y2=2px,则p=1.
分析 求出y2=4x',焦点坐标为(1,0),再利用平面α和β所成的二面角α-y轴-β等于60°,即可得出结论.
解答 解:β内的曲线C'的方程是y2=4x',焦点坐标为(1,0)
根据题意,得到$\frac{p}{2}$=1•cos60°,∴p=1.
故答案为1.
点评 本题考查平行投影,考查两个坐标系之间的坐标关系,是一个比较简单的题目,解答关键是找出两个坐标间的关系.

练习册系列答案
相关题目
11.已知直角坐标系中点A(0,1),向量$\overrightarrow{AB}=(-4,-3),\overrightarrow{BC}=(-7,-4)$,则点C的坐标为( )
| A. | (11,8) | B. | (3,2) | C. | (-11,-6) | D. | (-3,0) |
16.住在狗熊岭的7只动物,它们分别是熊大,熊二,吉吉,毛毛,蹦蹦,萝卜头,图图.为了更好的保护森林,它们要选出2只动物作为组长,则熊大,熊二至少一个被选为组长的概率为( )
| A. | $\frac{11}{42}$ | B. | $\frac{1}{2}$ | C. | $\frac{11}{21}$ | D. | $\frac{10}{21}$ |
6.直线$x+\sqrt{3}y-1=0$的倾斜角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
11.曲线C1:y=sinx,曲线${C_2}:{x^2}+{(y+r-\frac{1}{2})^2}={r^2}$(r>0),它们交点的个数( )
| A. | 恒为偶数 | B. | 恒为奇数 | C. | 不超过2017 | D. | 可超过2017 |
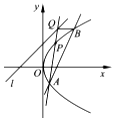 已知直线l的方程为y=x+2,点P是抛物线y2=4x上到直线l距离最小的点,点A是抛物线上异于点P的点,直线AP与直线l交于点Q,过点Q与x轴平行的直线与抛物线y2=4x交于点B.
已知直线l的方程为y=x+2,点P是抛物线y2=4x上到直线l距离最小的点,点A是抛物线上异于点P的点,直线AP与直线l交于点Q,过点Q与x轴平行的直线与抛物线y2=4x交于点B.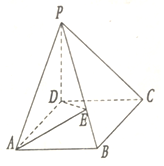 如图在棱锥P-ABCD中,ABCD为矩形,PD⊥面ABCD,PB=2,PB与面PCD成45°角,PB与面ABD成30°角.
如图在棱锥P-ABCD中,ABCD为矩形,PD⊥面ABCD,PB=2,PB与面PCD成45°角,PB与面ABD成30°角.