题目内容
18．
如图，在三棱锥S-ABC中，△ABC为直角三角形，且∠ACB=90°，SA⊥平面ABC，AD⊥SC．求证：AD⊥平面SBC．
分析 要证线面垂直，关键要找到两条相交直线与之都垂直，先由线面垂直得线线垂直，然后利用线面垂直的判定得线面垂直继而得到线线垂直AD⊥BC，问题从而得证．
解答 证明：∵∠ACB=90°，
∴BC⊥AC．
又SA⊥面ABC，
∴SA⊥BC，
∴BC⊥面SAC，
∴BC⊥AD．
又SC⊥AD，SC∩BC=C，
∴AD⊥面SBC．
点评 本题考查了线面垂直的判定和线面垂直的定义的应用，考查了学生灵活进行垂直关系的转化，是个基础题．
练习册系列答案
相关题目
8．设函数f（x）=ex（3x-1）-ax+a，其中a＜1，若有且只有一个整数x0使得f（x0）≤0，则a的取值范围是（ ）
| A． | $（\frac{2}{e}，\frac{3}{4}）$ | B． | $[\frac{2}{e}，\frac{3}{4}）$ | C． | $（\frac{2}{e}，1）$ | D． | $[\frac{2}{e}，1）$ |
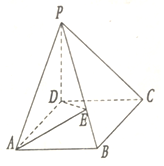如图在棱锥P-ABCD中，ABCD为矩形，PD⊥面ABCD，PB=2，PB与面PCD成45°角，PB与面ABD成30°角．
6．直线$x+\sqrt{3}y-1=0$的倾斜角为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |