Question

8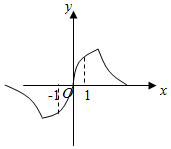．若函数f（x）=$\frac{（2-m）x}{{x}^{2}+m}$的图象如图所示，则m的范围为（　　）

• A． （-∞，-1）
• B． （-1，2）
• C． （0，2）
• D． （1，2）

Answer 1

分析 根据函数的极值点范围和函数值的符号判断．

解答 解：∵当x＞0时，f（x）＞0，∴2-m＞0，故m＜2．
f′（x）=$\frac{（2-m）（m-{x}^{2}）}{（{x}^{2}+m）^{2}}$．
∵f（x）有两个绝对值大于1的极值点，∴m-x²=0有两个绝对值大于1的解，
∴m＞1．
故选：D．

点评 本题考查了函数图象的判断，通常从函数的单调性，奇偶性，特殊点，极限等方面进行判断．