题目内容
16.函数f(x)=x3-3x-1,若对于区间[-3,4]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是70.分析 对于区间[-3,4]上的任意x1,x2都有|f(x1)-f(x2)|≤t,等价于对于区间[-3,4]上的任意x,都有f(x)max-f(x)min≤t,利用导数确定函数的单调性,求最值,即可得出结论.
解答 解:对于区间[-3,4]上的任意x1,x2都有|f(x1)-f(x2)|≤t,等价于对于区间[-3,4]上的任意x,都有f(x)max-f(x)min≤t,
∵f(x)=x3-3x-1,∴f′(x)=3x2-3=3(x-1)(x+1),
∵x∈[-3,4],
∴函数在[-3,-1]、[1,4]上单调递增,在[-1,1]上单调递减;
∴f(x)max=f(4)=51,f(x)min=f(-3)=-19;
∴f(x)max-f(x)min=70,
∴t≥70;
∴实数t的最小值是70.
故答案为:70.
点评 本题考查导数知识的运用,考查恒成立问题,正确求导,确定函数的最值是关键.

练习册系列答案
相关题目
8.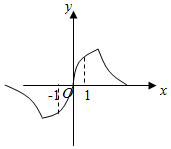 若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
 若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )| A. | (-∞,-1) | B. | (-1,2) | C. | (0,2) | D. | (1,2) |
6.在三棱锥S-ABC中,E,F分别为SB,SC上的点,且EF∥面ABC,则( )
| A. | EF与BC相交 | B. | EF∥BC | C. | EF与BC异面 | D. | 以上均有可能 |
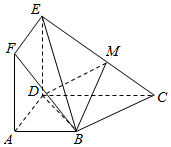 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,$AB=AD=\frac{1}{2}CD=2$,$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$.
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,$AB=AD=\frac{1}{2}CD=2$,$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$.