题目内容
18.已知常数a≠0,f(x)=alnx+2x.(1)当a=-4时,求f(x)的极值;
(2)当f(x)的最小值不小于-a时,求实数a的取值范围.
分析 (1)求出f(x)的导数,得到函数的单调区间,求出函数的极小值即可;
(2)问题转化为alnx+2x+a≥0,令g(x)=alnx+2x+a,g′(x)=$\frac{a}{x}$+2,通过讨论g(x)的单调性,求出a的范围即可.
解答 解:(1)f(x)的定义域是(0,+∞),
a=-4时,f(x)=-4lnx+2x,
f′(x)=2-$\frac{4}{x}$=$\frac{2x-4}{x}$,
令f′(x)>0,解得:x>2,令f′(x)<0,解得:x<2,
∴f(x)在(0,2)递减,在(2,+∞)递增,
∴f(x)极小值=f(2)=4-4ln2;
(2)f(x)的最小值不小于-a,
即alnx+2x+a≥0,
令g(x)=alnx+2x+a,g′(x)=$\frac{a}{x}$+2,
a≥0时,g(x)在(0,+∞)递增,无最小值,不合题意,
a<0时,令g′(x)>0,解得:x>-$\frac{a}{2}$,令g′(x)<0,解得:x<-$\frac{a}{2}$,
∴g(x)在(0,-$\frac{a}{2}$)递减,在(-$\frac{a}{2}$,+∞)递增,
∴g(x)最小值=g(-$\frac{a}{2}$)=aln(-$\frac{a}{2}$)≥0,
解得:-2≤a<0.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
8.已知集合A={x|1≤x≤4,x∈N},B={y|y=x2,x∈A},则A∩B=( )
| A. | {1,4} | B. | {2,3} | C. | {9,16} | D. | {1,2} |
9.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角性”.

该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )

该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
| A. | 2017×22015 | B. | 2017×22014 | C. | 2016×22015 | D. | 2016×22014 |
6.过椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的焦点F作直线l交椭圆C于P,Q两点.若|FP|=p,|FQ|=q,则$\frac{1}{p}$+$\frac{1}{q}$=( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
3.设A、B分别为(1+x)n展开式中的奇数项之和与偶数项之和,则A2-B2的值为( )
| A. | (1+x)2n | B. | (1-x)n | C. | (1-x2)n | D. | 2n+1 |
8.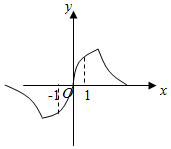 若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
 若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )| A. | (-∞,-1) | B. | (-1,2) | C. | (0,2) | D. | (1,2) |