题目内容
16．若函数y=x2+2（a-b）x+a2与x轴有两个交点，且b＞0，则a与b的关系是a＜$\frac{b}{2}$．分析 转化为方程有两个不同的根，从而可得△=[2（a-b）]2-4a2＞0，从而解不等式即可．
解答 解：∵函数y=x2+2（a-b）x+a2与x轴有两个交点，
∴△=[2（a-b）]2-4a2＞0，
即（a-b-a）（a-b+a）＞0，
即-b（2a-b）＞0，
∵b＞0，
∴2a-b＜0，
∴a＜$\frac{b}{2}$，
故答案为：a＜$\frac{b}{2}$．
点评 本题考查了二次函数的性质的应用及二次方程的根的个数的判断，同时考查了转化思想的应用．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
6．过椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的焦点F作直线l交椭圆C于P，Q两点．若|FP|=p，|FQ|=q，则$\frac{1}{p}$+$\frac{1}{q}$=（ ）
| A． | 3 | B． | $\frac{3}{2}$ | C． | $\frac{4}{3}$ | D． | $\frac{5}{4}$ |
8．
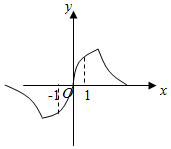若函数f（x）=$\frac{（2-m）x}{{x}^{2}+m}$的图象如图所示，则m的范围为（ ）
若函数f（x）=$\frac{（2-m）x}{{x}^{2}+m}$的图象如图所示，则m的范围为（ ）| A． | （-∞，-1） | B． | （-1，2） | C． | （0，2） | D． | （1，2） |
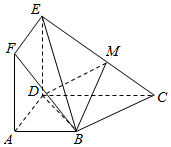如图所示，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，$AB=AD=\frac{1}{2}CD=2$，$\overrightarrow{EM}=λ\overrightarrow{EC}（0＜λ＜1）$．