题目内容
13．在数列{an}中．a1=4．a2=10．若数列{log3（an-1）}为等差数列，则Tn=a1+a2+…+an-n=$\frac{{3}^{n+1}-3}{2}$．分析 由题意可判数列{an-1}为首项为3公比为$\frac{9}{3}$=3的等比数列，由等比数列的求和公式计算可得．
解答 解：∵数列{log3（an-1）}为等差数列，
∴log3（an+1-1）-log3（an-1）=d，（d为公差），
∴log3$\frac{{a}_{n+1}-1}{{a}_{n}-1}$=d，即$\frac{{a}_{n+1}-1}{{a}_{n}-1}$=3d，
∴数列{an-1}为等比数列，
由a1=4，a2=10可得a1-1=3，a2-1=9，
∴数列{an-1}为首项为3公比为$\frac{9}{3}$=3的等比数列，
∴an-1=3×3n-1=3n，∴an=3n+1，
∴Tn=a1+a2+…+an-n=$\frac{3×（1-{3}^{n}）}{1-3}$=$\frac{{3}^{n+1}-3}{2}$
故答案为：$\frac{{3}^{n+1}-3}{2}$
点评 本题考查等比数列的求和公式，涉及等比数列的判定，属基础题．
练习册系列答案
巧学巧练系列答案
相关题目
3．设A、B分别为（1+x）n展开式中的奇数项之和与偶数项之和，则A2-B2的值为（ ）
| A． | （1+x）2n | B． | （1-x）n | C． | （1-x2）n | D． | 2n+1 |
8．
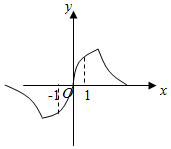若函数f（x）=$\frac{（2-m）x}{{x}^{2}+m}$的图象如图所示，则m的范围为（ ）
若函数f（x）=$\frac{（2-m）x}{{x}^{2}+m}$的图象如图所示，则m的范围为（ ）| A． | （-∞，-1） | B． | （-1，2） | C． | （0，2） | D． | （1，2） |