题目内容
19.在极坐标系中,已知A(6,$\frac{π}{3}$),B(8,$\frac{4π}{3}$),则线段AB中点的极坐标是(1,$\frac{4π}{3}$).分析 求出中点的直角坐标,转化为极坐标.
解答 解:A的直角坐标为(6cos$\frac{π}{3}$,6sin$\frac{π}{3}$),即A(3,3$\sqrt{3}$).
B的直角坐标为(8cos$\frac{4π}{3}$,8sin$\frac{4π}{3}$),即B(-4,-4$\sqrt{3}$).
∴AB的中点C坐标为(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$).
∴C点的极坐标为(1,$\frac{4π}{3}$).
故答案为(1,$\frac{4π}{3}$).
点评 本题考查了点的极坐标与直角坐标的转化,属于基础题.

练习册系列答案
相关题目
9.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角性”.

该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )

该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
| A. | 2017×22015 | B. | 2017×22014 | C. | 2016×22015 | D. | 2016×22014 |
8.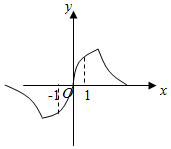 若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
 若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )| A. | (-∞,-1) | B. | (-1,2) | C. | (0,2) | D. | (1,2) |
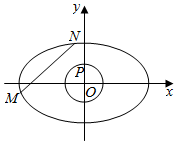 如图,已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,圆O:x2+y2=1,其中M,N是椭圆C上的两个动点,P是圆O上一个动点.
如图,已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,圆O:x2+y2=1,其中M,N是椭圆C上的两个动点,P是圆O上一个动点.