题目内容
3.已知a,b是互异的正数,A是a,b的等差中项,G是a,b的正的等比中项,A与G有无确定的大小关系?分析 由已知可得2A=a+b,G2=ab,(G>0).再利用基本不等式的性质即可得出.
解答 解:∵a,b是互异的正数,A是a,b的等差中项,G是a,b的正的等比中项,
∴2A=a+b,G2=ab,(G>0).
可得A=$\frac{a+b}{2}$,G=$\sqrt{ab}$.
∵$\frac{a+b}{2}$≥$\sqrt{ab}$.
∴A≥G.
点评 本题考查了等差数列与等比数列的通项公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
8.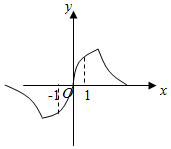 若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
 若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )
若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的范围为( )| A. | (-∞,-1) | B. | (-1,2) | C. | (0,2) | D. | (1,2) |
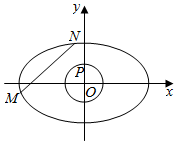 如图,已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,圆O:x2+y2=1,其中M,N是椭圆C上的两个动点,P是圆O上一个动点.
如图,已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,圆O:x2+y2=1,其中M,N是椭圆C上的两个动点,P是圆O上一个动点.