题目内容
若函数y=sin 2x的图象向左平移
个单位得到y=f(x)的图象,则( )
| π |
| 4 |
| A、f (x)=cos2x |
| B、f (x)=sin2x |
| C、f (x)=-cos2x |
| D、f (x)=-sin2x |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据三角函数图象之间的关系即可得到结论.
解答:
解:若函数y=sin 2x的图象向左平移
个单位得到y=sin2(x+
)=sin(2x+
)=cos2x,
故选:A
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
故选:A
点评:本题主要考查三角函数解析式的求解,根据函数的平移关系是解决本题的关键.

练习册系列答案
相关题目
过点A(4,a)和B(5,b)的直线与直线y=x+m平行,则|AB|的值是( )
| A、6 | ||
B、
| ||
| C、2 | ||
| D、1 |
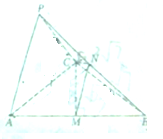 如图,在三棱锥P-ABC中,底面ABC是边长为4的正三角形,PA=PC=2
如图,在三棱锥P-ABC中,底面ABC是边长为4的正三角形,PA=PC=2