Question

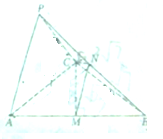如图，在三棱锥P-ABC中，底面ABC是边长为4的正三角形，PA=PC=2

3

，侧面PAC⊥底面ABC，M、N分别为AB、PB的中点
（1）求证：AC⊥PB；
（2）求空间几何体PAMNC的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系

专题：空间位置关系与距离

分析：（1）取AC中点E，连结PE，BE，由已知得PE⊥AC，BE⊥AC，由此能证明AC⊥PB．
（2）由V_PAMNC=V_P-ABC-V_N-BMC=

3

4

VP-ABC，能求出空间几何体PAMNC的体积．

解答： （1）证明：取AC中点E，连结PE，BE，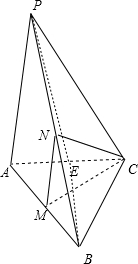
∵底面ABC是边长为4的正三角形，PA=PC=2

3

，
∴PE⊥AC，BE⊥AC，
∵PE∩BE=E，∴AC⊥平面BPE，
∵PB?平面BPE，∴AC⊥PB．
（2）解：V_PAMNC=V_P-ABC-V_N-BMC，
∵N为PB中点，∴N到平面MBC的高为

1

2

PE，
又S△BMC=

1

2

S△ABC，
∴VN-MBC=

1

4

VP-ABC，
∴V_PAMNC=V_P-ABC-V_N-BMC
=

3

4

VP-ABC
=

3

4

×

1

3

×2

2

×

1

2

×4×2

3

=2

6

．

点评：本题考查异面直线垂直的证明，考查几何体的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．