题目内容

12．下列命题中正确的是（　　）
A．$\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{AB}$B．$\overrightarrow{AB}$=$\overrightarrow{BA}$C．$\overrightarrow{0}$•$\overrightarrow{AB}$=$\overrightarrow{0}$D．$\overrightarrow{AB}+\overrightarrow{BC}$$+\overrightarrow{CD}$=$\overrightarrow{AD}$

分析 根据向量的加减的几何意义和向量的数量积运算即可判断

解答 解：$\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{BA}$，$\overrightarrow{AB}$=-$\overrightarrow{BA}$，$\overrightarrow{0}$•$\overrightarrow{AB}$=0，$\overrightarrow{AB}+\overrightarrow{BC}$$+\overrightarrow{CD}$=$\overrightarrow{AD}$，
故选：D

点评 本题考查了向量的加减的几何意义和向量的数量积运算，属于基础题．

练习册系列答案
相关题目
15．已知向量$\overrightarrow a=（{2cosα，{{sin}^2}α}），\overrightarrow b=（{2sinα，t}），α∈（{0，\frac{π}{2}}），t$为实数．
（1）若$\overrightarrow a-\overrightarrow b=（{\frac{2}{5}，0}）$，求t的值；
（2）若t=1，且$\overrightarrow a•\overrightarrow b=1$，求$tan（{2α+\frac{π}{4}}）$的值．
16．已知抛物线y2=8x上一点P到焦点的距离为4，则△PFO的面积为4．
13．已知函数f（x）=$\left\{\begin{array}{l}{{e}^{x}+ax，x≤0}\\{（4-a）x+2a，x＞0}\end{array}\right.$若对于任意两个不等实数x1，x2，都有$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞1成立，则实数a的取值范围是（　　）
A．[1，3）B．[$\frac{1}{2}$，3）C．[0，4）D．[$\frac{1}{2}$，4）
7．已知等轴双曲线C的一个焦点是F1（-6，0），点M是等轴双曲线的渐近线上的一个动点，点P是圆（x+6）2+y2=1上的任意一点，则|PM|的最小值是（　　）
A．3$\sqrt{2}$-1B．2$\sqrt{3}$-1C．3$\sqrt{3}$+1D．2$\sqrt{3}$+2
17．已知f（x）=|x-a|，a∈R．
（1）当a=1时，求不等式f（x）+|2x-5|≥6的解集；
（2）若函数g（x）=f（x）-|x-3|的值域为A，且[-1，2]⊆A，求a的取值范围．
4．已知实数x，y满足$\left\{\begin{array}{l}{2x-y+6≥0}\\{x+y≥0}\\{x≤2}\end{array}\right.$，若目标函数z=-mx+y的最大值为-2m+10，最小值为-2m-2，则实数m的取值不可能是（　　）
A．3B．2C．0D．-1
1．已知曲线$y=\frac{1}{4}{x^2}-3lnx$的一条切线的斜率为$-\frac{1}{2}$，则切点的横坐标为（　　）
A．-3B．2C．-3或2D．$\frac{1}{2}$
2．函数$f（x）=\frac{1}{2}cos（ωx+φ）$（ω＞0，$|φ|＜\frac{π}{2}$）的部分图象如图所示，则φ的值为（　　）
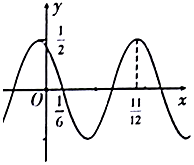
A．$\frac{π}{3}$B．$\frac{π}{6}$C．$-\frac{π}{6}$D．$-\frac{π}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网