题目内容
1.已知曲线$y=\frac{1}{4}{x^2}-3lnx$的一条切线的斜率为$-\frac{1}{2}$,则切点的横坐标为( )| A. | -3 | B. | 2 | C. | -3或2 | D. | $\frac{1}{2}$ |
分析 求出导数,设出切点,可得切线的斜率,解方程可得切点的横坐标.
解答 解:设切点为(m,n),(m>0),
$y=\frac{1}{4}{x^2}-3lnx$的导数为y′=$\frac{1}{2}$x-$\frac{3}{x}$,
可得切线的斜率为$\frac{1}{2}$m-$\frac{3}{m}$=-$\frac{1}{2}$,
解方程可得,m=2.
故选B.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,正确求导是解题的关键,属于基础题.

练习册系列答案
相关题目
12.下列命题中正确的是( )
| A. | $\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{AB}$ | B. | $\overrightarrow{AB}$=$\overrightarrow{BA}$ | C. | $\overrightarrow{0}$•$\overrightarrow{AB}$=$\overrightarrow{0}$ | D. | $\overrightarrow{AB}+\overrightarrow{BC}$$+\overrightarrow{CD}$=$\overrightarrow{AD}$ |
13.函数y=e-|lnx|-|2-x|的图象大致为( )
| A. | 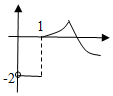 | B. | 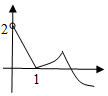 | C. | 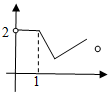 | D. | 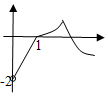 |
 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.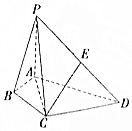 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.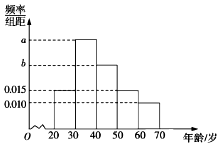 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.