题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x}+ax,x≤0}\\{(4-a)x+2a,x>0}\end{array}\right.$若对于任意两个不等实数x1,x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>1成立,则实数a的取值范围是( )| A. | [1,3) | B. | [$\frac{1}{2}$,3) | C. | [0,4) | D. | [$\frac{1}{2}$,4) |
分析 构造函数F(x)=f(x)-x,则F(x)为增函数,列不等式组解出a的范围.
解答 解:不妨设x1<x2,则x1-x2<0,则f(x1)-f(x2)<x1-x2,
∴f(x1)-x1<f(x2)-x2,
令F(x)=f(x)-x=$\left\{\begin{array}{l}{{e}^{x}+(a-1)x,x≤0}\\{(3-a)x+2a,x>0}\end{array}\right.$,则F(x)为增函数,
∴当x≤0时,F′(x)=ex+(a-1)≥0恒成立,即a≥1-ex在(-∞,0]上恒成立,
由y=1-ex在(-∞,0]上单调递减,且x→-∞时,1-ex→1,
∴a≥1,
当x>0时,F(x)是一次函数,故3-a>0,即a<3,
又F(x)在R上是增函数,∴1≤2a,即a≥$\frac{1}{2}$.
综上,1≤a<3.
故选A.
点评 本难题考查了分段函数的单调性,函数单调性的判断,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
3.已知集合A={x|(x-6)(3x+8)<0},B={x|y=$\sqrt{x+1}$},则A∩B等于( )
| A. | [-1,6) | B. | (-1,6) | C. | (-$\frac{8}{3}$,-1] | D. | (-$\frac{8}{3}$,-1) |
8.已知定义在R上的奇函数f(x)满足当x≥0时,f(x)=1og2(x+2)+x+b,则|f(x)|>3的解集为( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-,4)∪(4,+∞) | C. | (-2,2) | D. | (-4,4) |
5.在△ABC中,a,b,c分别是角A、B、C所对的边长,A、B均为锐角,若sinA=cosB,则$\frac{a+b}{c}$的最大值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
12.下列命题中正确的是( )
| A. | $\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{AB}$ | B. | $\overrightarrow{AB}$=$\overrightarrow{BA}$ | C. | $\overrightarrow{0}$•$\overrightarrow{AB}$=$\overrightarrow{0}$ | D. | $\overrightarrow{AB}+\overrightarrow{BC}$$+\overrightarrow{CD}$=$\overrightarrow{AD}$ |
 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.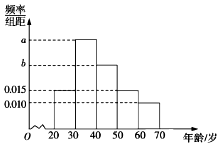 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.