题目内容
17.已知f(x)=|x-a|,a∈R.(1)当a=1时,求不等式f(x)+|2x-5|≥6的解集;
(2)若函数g(x)=f(x)-|x-3|的值域为A,且[-1,2]⊆A,求a的取值范围.
分析 (1)将a=1代入f(x),通过讨论x的范围求出各个区间上的x的范围,取并集即可;
(2)通过讨论a的范围,得到关于a的不等式组,解出即可.
解答 解:(1)a=1时,|x-1|+|2x-5|≥6,
x≤1时:1-x-2x+5≥6,解得:x≤0,∴x≤0,
1<x<2.5时:x-1-2x+5≥6,解得:x≤-1,不成立;
x≥2.5时:x-1+2x-5≥6,解得:x≥4,∴x≥4,
故不等式的解集是{x|x≥4或x≤0};
(2)g(x)=|x-a|-|x-3|,
a≥3时:g(x)=$\left\{\begin{array}{l}{3-a,x≥a}\\{a+3-2x,3<x<a}\\{a-3,x≤3}\end{array}\right.$,
∴3-a≤g(x)≤a-3,
∵[-1,2]⊆A,∴$\left\{\begin{array}{l}{3-a≤-1}\\{a-3≥2}\end{array}\right.$,解得a≥5;
a<3时,a-3≤g(x)≤3-a,
∴$\left\{\begin{array}{l}{a-3≤-1}\\{3-a≥2}\end{array}\right.$,解得:a≤1;
综上:a≤1或a≥5.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
20.已知x>y,则下列不等式一定成立的是( )
| A. | $\frac{1}{x}<\frac{1}{y}$ | B. | log2(x-y)>0 | C. | x3<y3 | D. | ${(\frac{1}{2})^x}<{(\frac{1}{2})^y}$ |
5.在△ABC中,a,b,c分别是角A、B、C所对的边长,A、B均为锐角,若sinA=cosB,则$\frac{a+b}{c}$的最大值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
12.下列命题中正确的是( )
| A. | $\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{AB}$ | B. | $\overrightarrow{AB}$=$\overrightarrow{BA}$ | C. | $\overrightarrow{0}$•$\overrightarrow{AB}$=$\overrightarrow{0}$ | D. | $\overrightarrow{AB}+\overrightarrow{BC}$$+\overrightarrow{CD}$=$\overrightarrow{AD}$ |
7.已知$α∈R,sinα+2cosα=\frac{{\sqrt{10}}}{2}$,则tan2α=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
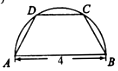 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的周长的最大值为10. 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.