题目内容

16．已知抛物线y2=8x上一点P到焦点的距离为4，则△PFO的面积为4．

分析 利用抛物线的定义，求出P的坐标，然后求出三角形的面积．

解答 解：由抛物线定义，|PF|=xP+2=4，所以xP=2，|yP|=4，
所以，△PFO的面积S=$\frac{1}{2}$|OF||yP|=$\frac{1}{2}$×2×4=4．
故答案为：4．

点评 本题考查抛物线的简单性质的应用，三角形的面积的求法，考查计算能力．

练习册系列答案
相关题目
6．已知A={x|-4＜x＜1}，B={x|x2-x-6＜0}，则A∪B等于（　　）
A．（-3，1）B．（-2，1）C．（-4，2）D．（-4，3）
7．已知等比数列{an}为递增数列，Sn是其前n项和．若a1+a5=$\frac{17}{2}$，a2a4=4，则S6=（　　）
A．$\frac{27}{16}$B．$\frac{27}{8}$C．$\frac{63}{4}$D．$\frac{63}{2}$
4．已知$\frac{1}{1+i}=\frac{1}{2}$-ni其中n是实数，i是虚数单位，那么n=$\frac{1}{2}$．
11．设函数f（x）=（x-a）•ex，a∈R．
（Ⅰ）当a=1时，试求f（x）的单调增区间；
（Ⅱ）试求f（x）在[1，2]上的最大值；
（Ⅲ）当a=1时，求证：对于?x∈[-5，+∞），$f（x）+x+5≥-\frac{6}{e^5}$恒成立．
1．已知椭圆${C_1}：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的顶点到直线l：y=x的距离分别为$\frac{{\sqrt{6}}}{2}，\frac{{\sqrt{2}}}{2}$．
（1）求椭圆C1的离心率；
（2）过圆O：x2+y2=4上任意一点P作椭圆C1的两条切线PM和PN分别与圆交于点M，N，求△PMN面积的最大值．
8．已知定义在R上的奇函数f（x）满足当x≥0时，f（x）=1og2（x+2）+x+b，则|f（x）|＞3的解集为（　　）
A．（-∞，-2）∪（2，+∞）B．（-∞，-，4）∪（4，+∞）C．（-2，2）D．（-4，4）
12．下列命题中正确的是（　　）
A．$\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{AB}$B．$\overrightarrow{AB}$=$\overrightarrow{BA}$C．$\overrightarrow{0}$•$\overrightarrow{AB}$=$\overrightarrow{0}$D．$\overrightarrow{AB}+\overrightarrow{BC}$$+\overrightarrow{CD}$=$\overrightarrow{AD}$
13．函数y=e-|lnx|-|2-x|的图象大致为（　　）
A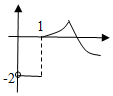．B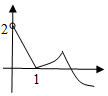．C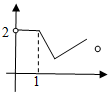．D．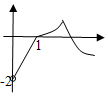

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网